5N
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 7 2021
Ta có: \(S=x^2+2xy+y^2-6x-6y+25\)
\(=\left(x+y\right)^2-6\left(x+y\right)+25\)
\(=\left(x+y\right)\left(x+y-6\right)+25\)
\(=3\cdot\left(3-6\right)+25\)
=-9+25
=16
25 tháng 12 2021
\(a,=5\left(x^2+2xy+y^2\right)-10y^2+5=5\left(x+y\right)^2-10y^2+5\\ =5\left(1+2\right)^2-10\cdot4+5=45-40+5=10\\ b,=7\left(x-y\right)-\left(x-y\right)^2=\left(x-y\right)\left(7-x+y\right)\\ =\left(2-2\right)\left(7-2+2\right)=0\)
25 tháng 12 2021
b: \(=7\left(x-y\right)-\left(x-y\right)^2\)
\(=\left(x-y\right)\left(7-x+y\right)=0\)
18 tháng 10 2021
\(a,A=\left(x+y\right)^2-9z^2=\left(x+y-3z\right)\left(x+y+3z\right)\\ A=\left(5+7-36\right)\left(5+7+36\right)=-24\cdot48=-1152\\ b,B=\left(2x-y\right)\left(2x+y\right)+\left(2x+y\right)=\left(2x+y\right)\left(2x-y-1\right)\\ B=\left(2+2\right)\left(2-2-1\right)=4\cdot\left(-1\right)=-4\)
12 tháng 11 2021
\(=\left(x-y\right)^2+x=\left(25-5\right)^2+25=20^2+25=400+25=425\)
12 tháng 11 2021
x2-2xy+y2+x
= (x-y)2+ x
thay số:
= (25-5)2+ 25
= 202+25
= 400+25
= 425
Vậy biểu thức có giá trị là 425 khi x=25 và y=5.
NN
1
H9
HT.Phong (9A5)
CTVHS
20 tháng 8 2023
a) \(N=x^2-10x+25\)
\(N=x^2-2\cdot5\cdot x+5^2\)
\(N=\left(x-5\right)^2\)
Thay x = 55 vào N ta có:
\(N=\left(55-5\right)^2=2500\)
b) \(P=\dfrac{x^4}{4}-x^2y+y^2\)
\(P=\left(\dfrac{x^2}{2}\right)^2-2\cdot\dfrac{x^2}{2}\cdot y+y^2\)
\(P=\left(\dfrac{x^2}{2}-y\right)^2\)
Thay x = 4 và \(y=\dfrac{1}{2}\) vào P ta có:
\(P=\left(\dfrac{4^2}{2}-\dfrac{1}{2}\right)^2=\dfrac{225}{4}\)
20 tháng 8 2023
Phần b mình thấy kết quả nó sai b ạ thầy cho mình đáp án là 225/9
LV
1
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 4 2021
\(A=x^2+y^2+\left(\dfrac{1}{2}\right)^2-2xy+2.\dfrac{1}{2}x-2.\dfrac{1}{2}.y+\dfrac{3}{4}\)
\(A=\left(x-y+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
\(A_{min}=\dfrac{3}{4}\) khi \(x-y+\dfrac{1}{2}=0\)
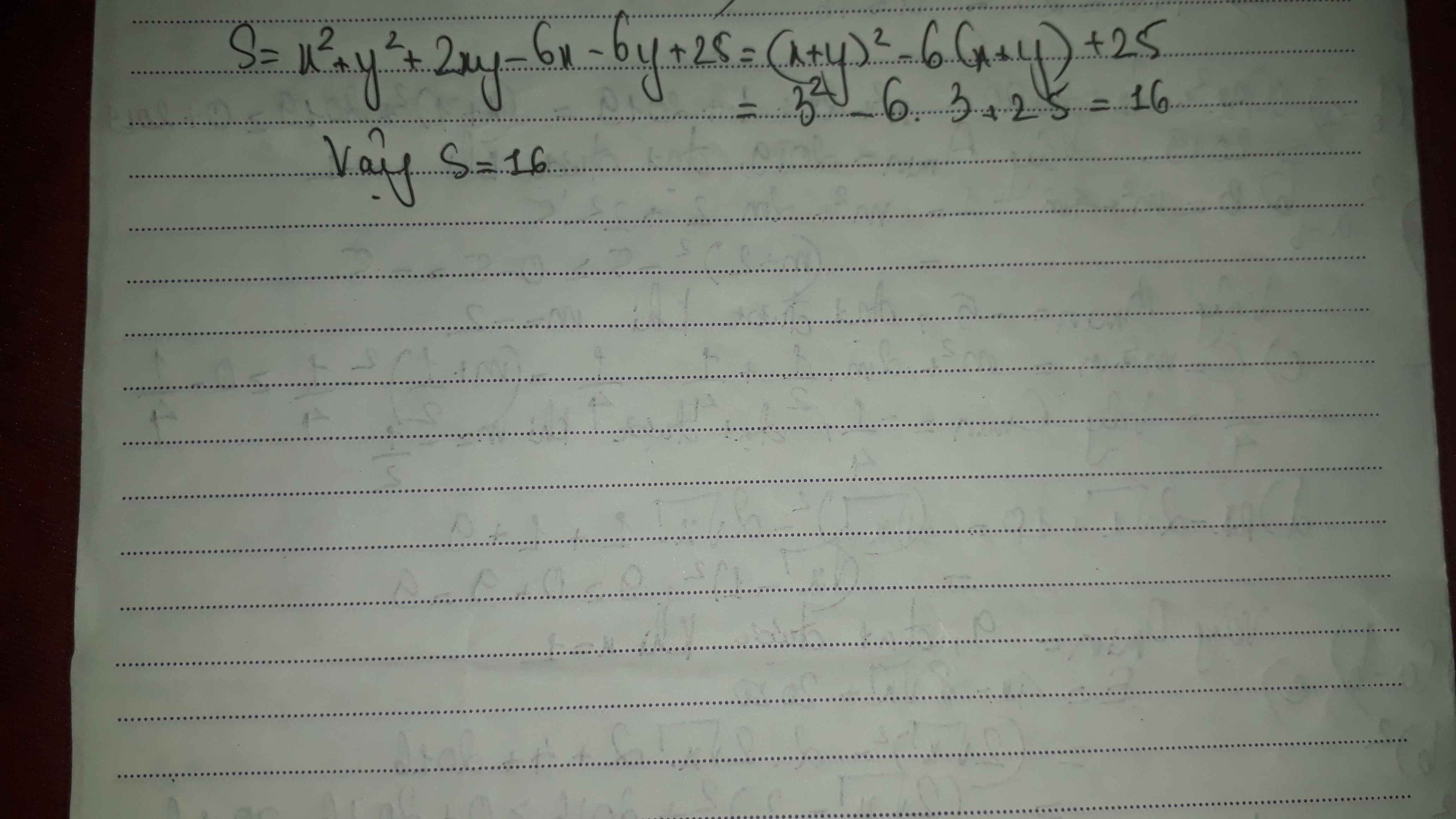
\(=\left(x-y\right)^2+x=\left(25-5\right)^2+5=20^2+5=405\)