
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trong toán học, một tập hợp hữu hạn là một tập hợp có một số hữu hạn các phần tử. Một cách không chính thức, một tập hữu hạn là một tập hợp mà có thể đếm và có thể kết thúc việc đếm. Ví dụ,
là một tập hợp hữu hạn có 5 phần tử. Số phần tử của một tập hợp hữu hạn là một số tự nhiên (một số nguyên không âm) và được gọi là lực lượng của tập hợp đó. Một tập hợp mà không hữu hạn được gọi là tập hợp vô hạn. Ví dụ, tập hợp tất cả các số nguyên dương là vô hạn:
Tập hợp hữu hạn đặc biệt quan trọng trong toán học tổ hợp, môn toán học nghiên cứu về phép đếm. Nhiều bài toán liên quan đến các tập hữu hạn dựa vào nguyên lý ngăn kéo Dirichlet, chỉ ra rằng không thể tồn tại một đơn ánh từ một tập hợp hữu hạn lớn hơn vào một tập hợp hữu hạn nhỏ hơn.

Chỉ với những điều kiện như em nêu thì biểu thức này không rút gọn thêm được.
Còn việc bé hơn hoặc bằng một biểu thức nào khác thì có nhiều. Tốt nhất em nên nêu cụ thể đề để được hỗ trợ tốt hơn.


Bài 1
Mình làm mẫu một số câu thôi nhé
\(9,\sqrt{5}=\left(\sqrt{5}\right)^2=5\\ \sqrt{6}=\left(\sqrt{6}\right)^2=6\)
Vì \(5< 6\)
\(\Rightarrow\sqrt{5}< \sqrt{6}\)
\(10,2\sqrt{5}=\left(2\sqrt{5}\right)^2=20\\ \sqrt{7}=\left(\sqrt{7}\right)^2=7\)
Vì \(20>7\)
\(\Rightarrow2\sqrt{5}>\sqrt{7}\)
\(11,5\sqrt{2}=\left(5\sqrt{2}\right)^2=50\\ 2\sqrt{3}=\left(2\sqrt{3}\right)^2=12\)
Vì \(50>12\Rightarrow5\sqrt{2}>2\sqrt{3}\)
\(12,2\sqrt{6}=\left(2\sqrt{6}\right)^2=24\\ 5=5^2=25\)
Vì \(25>24\Rightarrow5>2\sqrt{6}\)
\(13,\sqrt{7}=\left(\sqrt{7}\right)^2=7\\ 2=2^2=4\)
Vì \(7>4\Rightarrow\sqrt{7}>2\)
\(14,3=3^2=9\\ \sqrt{5}=\left(\sqrt{5}\right)^2=5\)
Vì \(9>5\Rightarrow3>\sqrt{5}\)
\(15,3\sqrt{6}=\left(3\sqrt{6}\right)^2=54\)
Vì \(54>1\Rightarrow3\sqrt{6}>1\)
\(16,2\sqrt{2}=\left(2\sqrt{2}\right)^2=8\\ 3=3^2=9\)
Vì \(8< 9\Rightarrow2\sqrt{2}< 3\)
Phương pháp làm dạng bài này là bình phương hai vế rồi so sánh
Bài 2
Gợi ý : Biểu thức dưới dấu căn \(\ge\) 0
Lưu ý : Nếu biểu thức dưới dấu căn ở dưới mẫu thì \(>0\)
\(21,ĐK:4x^2-12x+9>0\\ \Rightarrow\left(2x-3\right)^2>0\\ \Leftrightarrow x\ne\dfrac{3}{2}\)
\(22,ĐK:x^2-8x+15\ge0\\ \Rightarrow\left[{}\begin{matrix}x\le3\\x\ge5\end{matrix}\right.\)
\(23,ĐK:\left\{{}\begin{matrix}x-2\ge0\\x-5\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ge2\\x\ne5\end{matrix}\right.\)
\(24,ĐK:\left\{{}\begin{matrix}\dfrac{2+x}{5-x}\ge0\\5-x\ne0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}2+x\ge0\\5-x\ge0\\x\ne5\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\ge-2\\x\le5\\x\ne5\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\ge-2\\x< 5\end{matrix}\right.\left(t/m\right)\)
Hoặc
\(\left\{{}\begin{matrix}2+x\le0\\5-x\le0\\5-x\ne0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\le-2\\x\ge5\\x\ne5\end{matrix}\right.\left(loại\right)\)

a)Trong toán học, đặc biệt là lý thuyết nhóm, các phần tử của một nhóm có thể được phân hoạch thành các lớp liên hợp; các phần tử của cùng một lớp liên hợp có nhiều tính chất chung, và việc nghiên cứu các lớp liên hợp của các nhóm không giao hoán cho ta biết nhiều đặc điểm quan trọng về cấu trúc của nhóm.
Ví dụ:
Xét một \(p-nhóm\) hữu hạn \(G\). Ta sẽ chứng minh rằng: mọi \(p-nhóm\) hữu hạn luôn có tâm không tầm thường.
Vì cấp của mọi lớp liên hợp của \(G\) phải chia hết cấp của \(G\) .Ta suy ra rằng mọi lớp liên hợp \(H_i\) có cấp \(p^{k_i}\) , với \(0< k_i< n\). Từ phương trình lớp ta suy ra:
Từ đây ta suy ra \(p\) là ước của \(|Z\left(G\right)|\), hay \(|Z\left(G\right)|\)\(>1\)
Tham khảo:
Trong toán học, đặc biệt là lý thuyết nhóm, các phần tử của một nhóm có thể được phân hoạch thành các lớp liên hợp; các phần tử của cùng một lớp liên hợp có nhiều tính chất chung, và việc nghiên cứu các lớp liên hợp của các nhóm không giao hoán cho ta biết nhiều đặc điểm quan trọng về cấu trúc của nhóm.
Ví dụ:
Xét một p−nhómp−nhóm hữu hạn GG. Ta sẽ chứng minh rằng: mọi p−nhómp−nhóm hữu hạn luôn có tâm không tầm thường.
Vì cấp của mọi lớp liên hợp của GG phải chia hết cấp của GG .Ta suy ra rằng mọi lớp liên hợp HiHi có cấp pkipki , với 0<ki<n0<ki<n. Từ phương trình lớp ta suy ra:
Từ đây ta suy ra pp là ước của |Z(G)||Z(G)|, hay |Z(G)||Z(G)|>1



\(P=\dfrac{2\sqrt{x}}{\sqrt{x}+3}\left(x\ge0\right)\)
để P>\(\dfrac{1}{4}< =>\dfrac{2\sqrt{x}}{\sqrt{x}+3}>\dfrac{1}{4} < =>\dfrac{2\sqrt{x}}{\sqrt{x}+3}-\dfrac{1}{4}>0\)
<=>\(\dfrac{4.2\sqrt{x}}{4\left(\sqrt{x}+3\right)}-\dfrac{\sqrt{x}+3}{4\left(\sqrt{x}+3\right)}>0\)
<=>\(\dfrac{8\sqrt{x}-\sqrt{x}-3}{4\left(\sqrt{x}+3\right)}>0< =>\dfrac{7\sqrt{x}-3}{4\left(\sqrt{x}+3\right)}>0\)
ta có \(\sqrt{x}\ge0\left(\forall x\right)=>\sqrt{x}+3\ge3=>4\left(\sqrt{x}+3\right)>12\)
hay \(4\left(\sqrt{x}+3\right)>0\)
vậy để \(\dfrac{7\sqrt{x}-3}{4\left(\sqrt{x}+3\right)}>0< =>7\sqrt{x}-3>0< =>7\sqrt{x}>3< =>\sqrt{x}>\dfrac{3}{7}\)
<=>\(x>\dfrac{9}{49}\)
vậy x>9/49 thì pP>1/4





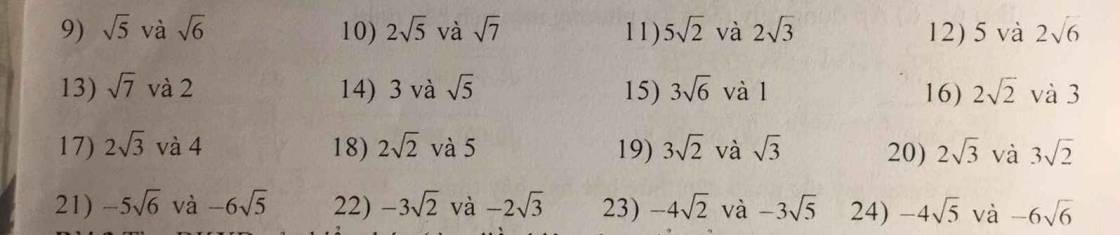
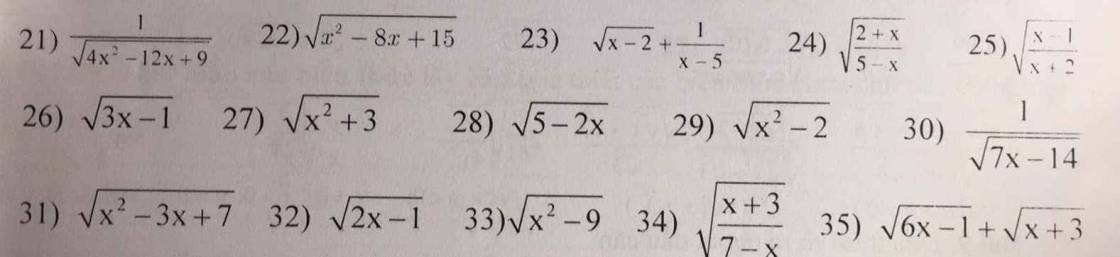


ĐKXĐ:
1 - x² ≥ 0 và x - 1 ≥ 0
⇔ x² ≤ 1 và x ≥ 1
⇔ -1 ≤ x ≤ 1 và x ≥ 1
⇔ x = 1