Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số cuộc gọi của người đó trong một tuần là \(n = 8 + 10 + 7 + 5 + 2 + 1 = 33\).
Gọi \({x_1};{x_2};...;{x_{33}}\) là thời gian thực hiện cuộc gọi của người đó trong một tuần được xếp theo thứ tự không giảm.
Ta có:
\({x_1},...,{x_8} \in \left[ {0;60} \right);{x_9},...,{x_{18}} \in \left[ {60;120} \right);{x_{19}},...,{x_{25}} \in \left[ {120;180} \right);{x_{26}},...,{x_{30}} \in \left[ {180;240} \right);\) \({x_{31}},{x_{32}} \in \left[ {240;300} \right);{x_{33}} \in \left[ {300;360} \right)\).
• Tứ phân vị thứ hai của dãy số liệu là: \({x_{17}}\) thuộc nhóm \(\begin{array}{*{20}{l}}{\left[ {60;120} \right)}\end{array}\)
Ta có: \(n = 33;{n_m} = 10;C = 8;{u_m} = 60;{u_{m + 1}} = 120\)
Tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 60 + \frac{{\frac{{33}}{2} - 8}}{{10}}.\left( {120 - 60} \right) = 111\)
• Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_8} + {x_9}} \right)\).
Do \({x_8} \in \left[ {0;60} \right),{x_9} \in \left[ {60;120} \right)\) nên tứ phân vị thứ nhất của dãy số liệu là: \({Q_1} = 60\).
• Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{25}} + {x_{26}}} \right)\).
Do \({x_{25}} \in \left[ {120;180} \right),{x_{26}} \in \left[ {180;240} \right)\) nên tứ phân vị thứ ba của dãy số liệu là: \({Q_3} = 180\).

Ta có:
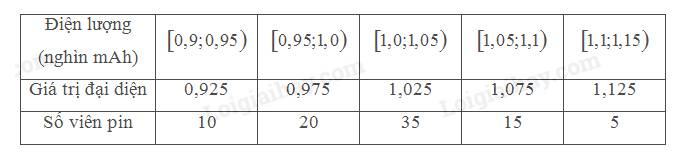
Tổng số viên pin là: \(n = 10 + 20 + 35 + 15 + 5 = 85\).
• Điện lượng trung bình của một số viên pin tiểu sau khi ghép nhóm là:
\(\bar x = \frac{{10.0,925 + 20.0,975 + 35.1,025 + 15.1,075 + 5.1,125}}{{85}} \approx 1,02\left( {mAh} \right)\)
• Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\begin{array}{*{20}{c}}{\left[ {1,0;1,05} \right)}\end{array}\).
Do đó: \({u_m} = 1,0;{n_{m - 1}} = 20;{n_m} = 35;{n_{m + 1}} = 15;{u_{m + 1}} - {u_m} = 1,05 - 1,0 = 0,05\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 1,0 + \frac{{35 - 20}}{{\left( {35 - 20} \right) + \left( {35 - 15} \right)}}.0,05 \approx 1,02\left( {mAh} \right)\)
Gọi \({x_1};{x_2};...;{x_{85}}\) là điện lượng của các viên pin được xếp theo thứ tự không giảm.
Ta có:
\(\begin{array}{l}{x_1},...,{x_{10}} \in \begin{array}{*{20}{c}}{\left[ {0,9;0,95} \right)}\end{array};{x_{11}},...,{x_{30}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {0,95;1,0} \right)}\end{array}}\end{array};{x_{31}},...,{x_{65}} \in \begin{array}{*{20}{c}}{\left[ {1,0;1,05} \right)}\end{array};\\{x_{66}},...,{x_{80}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {1,05;1,1} \right)}\end{array}}\end{array};{x_{81}},...,{x_{85}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {1,1;1,15} \right)}\end{array}}\end{array}}\end{array}\end{array}\)
• Tứ phân vị thứ hai của dãy số liệu là: \({x_{43}}\)
Ta có: \(n = 85;{n_m} = 35;C = 10 + 20 = 30;{u_m} = 1,0;{u_{m + 1}} = 1,05\)
Do \({x_{43}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {1,0;1,05} \right)}\end{array}}\end{array}}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 1,0 + \frac{{\frac{{85}}{2} - 30}}{{35}}.\left( {1,05 - 1,0} \right) \approx 1,02\)
• Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_{21}} + {x_{22}}} \right)\).
Ta có: \(n = 85;{n_m} = 20;C = 10;{u_m} = 0,95;{u_{m + 1}} = 1,0\)
Do \({x_{21}},{x_{22}} \in \begin{array}{*{20}{c}}{\left[ {0,95;1,0} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 0,95 + \frac{{\frac{{85}}{4} - 10}}{{20}}.\left( {1,0 - 0,95} \right) \approx 0,98\)
• Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{64}} + {x_{65}}} \right)\).
Ta có: \(n = 85;{n_j} = 35;C = 10 + 20 = 30;{u_j} = 1,0;{u_{j + 1}} = 1,05\)
Do \({x_{64}},{x_{65}} \in \begin{array}{*{20}{c}}{\left[ {1,0;1,05} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 1,0 + \frac{{\frac{{3.85}}{4} - 30}}{{35}}.\left( {1,05 - 1,0} \right) \approx 1,048\)

a: Cường độ trung bình là:
\(I\left(t\right)=\dfrac{Q\left(t\right)-Q\left(t0\right)}{t-t0}\)
b: Cho biết cường độ trung bình khi t chạy tới t0 thì ngày càng được thể hiện chính xác hơn, rõ ràng hơn.

Không gian mẫu: \(n\left(\Omega\right)=10!\)
Chọn 5 chữ số từ 6 chữ số còn lại (khác 0,3,6,8): có \(C_6^5\) cách
Hoán vị 6 chữ số (5 chữ số được chọn nói trên và số 8): \(6!\) cách
Tổng cộng: \(6!.C_6^5\) số
Xác suất: \(P=\dfrac{6!.C_6^5}{10!}=...\)

Tham khảo:
a)

b) Không thể tính chính xác, chúng ta chỉ có thể tinh số gần đúng thời gian tự học trung bình của các học sinh trong lớp
c) Giá trị đại diện của nhóm bằng trung bình giá trị đầu mút phải và trái của nhóm đó
Nhóm \( \ge 4.5\) là nhóm mở nên ta dựa theo nhóm gần đó nhất là nhóm [3;4.5) để lấy giá trị đại diện

Số trung binh của mẫu số liệu: : \(\bar x = \frac{{0.75 \times 8 + 2.25 \times 23 + 2.75 \times 6 + 5.25 \times 3}}{{40}} = 2.25\).

Công thức tổng quát của cường độ dòng điện tại thời gian t là:
\(I\left(t\right)=q'\left(t\right)=Q_0\cdot\omega\cdot cos\left(\omega t\right)\)
=>\(I\left(6\right)=10^{-8}\cdot10^6\cdot\pi\cdot cos\left(10^6\cdot pi\cdot6\right)=0.01\pi\left(A\right)\)





Tổng số lần sạc pin: \(n = 2 + 5 + 7 + 6 + 3 = 23\)
• Thời gian sử dụng trung bình từ lúc chị An sạc đầy pin điện thoại cho tới khi hết pin là: \(\bar x = \frac{{2.8 + 5.10 + 7.12 + 6.14 + 3.16}}{{23}} \approx 12,26\) (giờ)
b) Gọi \({x_1};{x_2};...;{x_{23}}\) là thời gian sử dụng từ lúc chị An sạc đầy pin điện thoại cho tới khi hết pin được xếp theo thứ tự không giảm.
Ta có:
\({x_1},{x_2} \in \begin{array}{*{20}{c}}{\left[ {7;9} \right)}\end{array};{x_3},...,{x_7} \in \begin{array}{*{20}{c}}{\left[ {9;11} \right)}\end{array};{x_8},...,{x_{14}} \in \begin{array}{*{20}{c}}{\left[ {11;13} \right)}\end{array};{x_{15}},...,{x_{20}} \in \begin{array}{*{20}{c}}{\left[ {13;15} \right)}\end{array};{x_{21}},{x_{22}},{x_{23}} \in \begin{array}{*{20}{c}}{\left[ {15;17} \right)}\end{array}\)
Tứ phân vị thứ nhất của dãy số liệu là: \({x_6}\).
Ta có: \(n = 23;{n_m} = 5;C = 2;{u_m} = 9;{u_{m + 1}} = 11\)
Do \({x_6} \in \begin{array}{*{20}{l}}{\left[ {9;11} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 9 + \frac{{\frac{{23}}{4} - 2}}{5}.\left( {11 - 9} \right) = 10,5\)
Vậy nhận định của chị An hợp lí.