K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TD
7
16 tháng 2 2022
Thuiii
Xin đấy đừng đăng linh tinh nữa, nhiễu r
Báo cáo nếu lm vậy 1 lần nữa
DH
7
ZT
3
28 tháng 9 2021
a,b tỉ lệ với x,y
ta có\(\dfrac{a}{x}=\dfrac{b}{y}=\dfrac{a+b}{x+y}=\dfrac{a-b}{x-y}\)
thay kết quả vào rồi tìm a và b
28 tháng 9 2021
Bước 1. Đưa về dạng cơ bản
Bước 2. Vẽ sơ đổ
Bước 3. Tìm số phần bằng nhau
Bước 4. Tìm số bé
Bước 5. Tìm số lớn
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
23 tháng 11 2023
2 tam giác AMK và tg BMK có
AM=BM; có chung đường cao từ K->AB nên
\(S_{AMK}=S_{BMK}=\dfrac{1}{2}S_{BKA}=\dfrac{1}{2}x50=25cm^2\)
2 tam giác ABN và tam giác CBN có chung đường cao từ B->AC nên
\(\dfrac{S_{ABN}}{S_{CBN}}=\dfrac{AN}{NC}=\dfrac{1}{2}\)
Hai tg ABN và tg CBN có chung BN nên
\(\dfrac{S_{ABN}}{S_{CBN}}=\) đường cao từ A->BN / đường cao từ C->BN \(=\dfrac{1}{2}\)
Hai tg BKA và tg BKC có chung BK nên
\(\dfrac{S_{BKA}}{S_{BKC}}=\) đường cao từ A->BN / đường cao từ C->BN \(=\dfrac{1}{2}\)
\(\Rightarrow S_{BKC}=2xS_{BKA}=2x50=100cm^2\)
\(\Rightarrow S_{BMC}=S_{BMK}+S_{BKC}=25+100=125cm^2\)
Hai tg BMC và tg AMC có chung đường cao từ C->AB nên
\(\dfrac{S_{BMC}}{S_{AMC}}=\dfrac{BM}{AM}=1\Rightarrow S_{BMC}=S_{AMC}=125cm^2\)
\(\Rightarrow S_{ABC}=S_{BMC}+S_{AMC}=125+125=250cm^2\)
IT
10
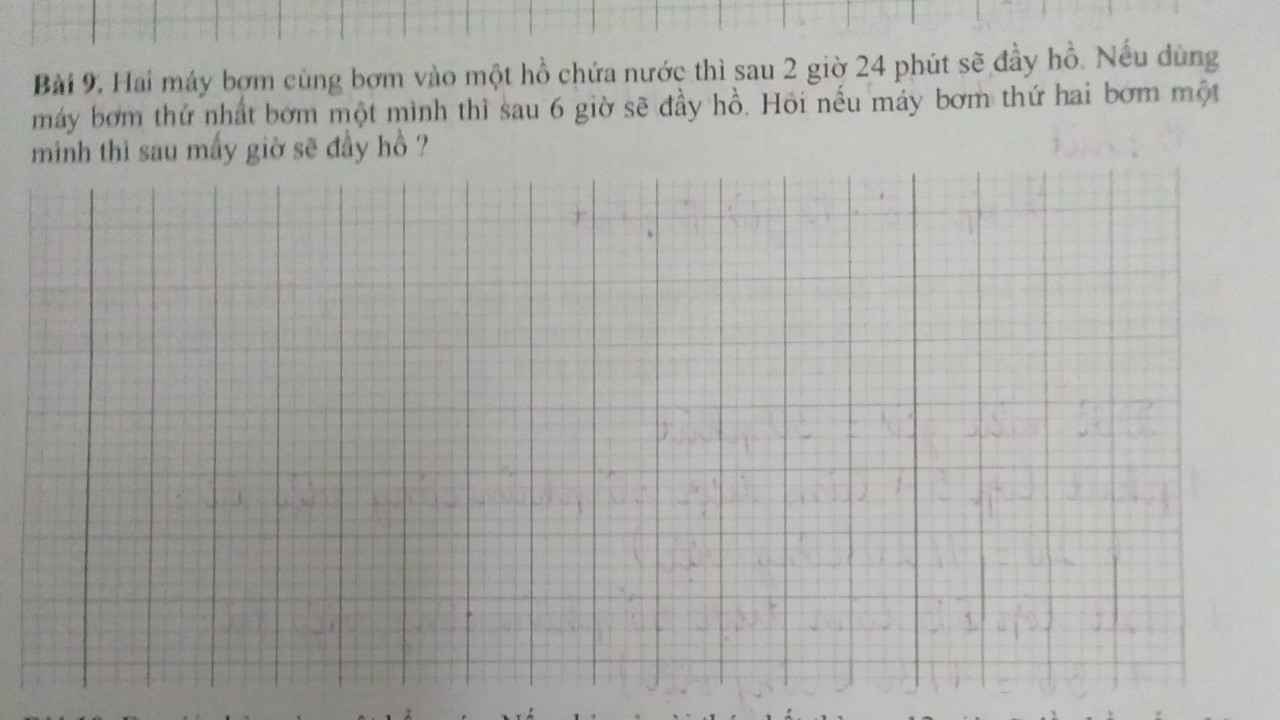
chắc bài dễ quá nên hông ai giúp tui ròi
chẳng nhẽ bài lớp 4 mà mn ko giúp tui sao~_~