
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐK \(x\ge-4\)
\(BPT\Leftrightarrow\hept{\begin{cases}2x-3\ge0\\x\ge-4\end{cases}\Leftrightarrow}\hept{\begin{cases}x\ge\frac{3}{2}\\x\ge-4\end{cases}}\)
\(\Rightarrow x\ge\frac{3}{2}\)
ĐK: \(x+4\ge0\) <=> \(x\ge-4\)
Bpt <=> \(\orbr{\begin{cases}x+4=0\\2x-3=0\end{cases}}\) hoặc \(2x-3>0\) <=> \(\orbr{\begin{cases}x=-4\\x=\frac{3}{2}\end{cases}}\)hoặc \(x>\frac{3}{2}\)
<=> \(\orbr{\begin{cases}x=-4\\x\ge\frac{3}{2}\end{cases}}\)Thỏa mãn đk.
Vậy
\(\orbr{\begin{cases}x=-4\\x\ge\frac{3}{2}\end{cases}}\)

chào tv mới
caua, 3x+x^2-4x=12
x^2-x-12=0
x^2-4x+3x-12=0
x(x-4)+3(x-4)=0
(x+3)(x-4)=0
x=-3 hoặc x=4
LƯU YS: từ chỗ mik biến đổi thành pt bậc 2 bn tính theo đenta cx đc, đây mik làm cách phân tích thành tích cho ngắn gọn

a)
\(\left(x+1\right)\left(x-3\right)\left(x^2-2x\right)=-2\)
<=> (x + 1).(x - 3).x.(x - 2) = -2
<=> [ (x + 1). (x - 3) ]. [ x. (x - 2) ] = -2
\(\Leftrightarrow\left(x^2-2x-3\right).\left(x^2-2x\right)+2=0\) (1)
Đặt \(x^2-2x=a\)
PT (1) <=> (a - 3).a + 2 = 0
\(\Leftrightarrow a^2-3a+2=0\)
\(\Leftrightarrow a^2-a-2a+2=0\)
<=> a. (a - 1) - 2. (a - 1) = 0
<=> (a - 1). (a - 2) = 0
<=> a - 1 = 0 hoặc a - 2 = 0
\(\Leftrightarrow\left[{}\begin{matrix}x^2-2x-1=0\\x^2-2x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(x-1\right)^2-2=0\\\left(x-1\right)^2-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(x-1-\sqrt{2}\right).\left(x-1+\sqrt{2}\right)=0\\\left(x-1-\sqrt{3}\right).\left(x-1+\sqrt{3}\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1+\sqrt{2}\\x=1-\sqrt{2}\\x=1+\sqrt{3}\\x=1-\sqrt{3}\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}x^2+x-y^2-y=0\left(1\right)\\x^2+y^2-2\left(x+y\right)=0\left(2\right)\end{matrix}\right.\)
PT (1)\(\Leftrightarrow\left(x-y\right)\left(x+y\right)+\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x+y+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=y\\x+y=-1\end{matrix}\right.\)
TH1: x=y thay vào Pt (2) ta được: \(2x^2-4x=0\Leftrightarrow\left[{}\begin{matrix}x=0\Rightarrow y=0\\x=2\Rightarrow y=2\end{matrix}\right.\)
TH2: Thay x+y=-1 vào Pt (2) ta được: \(x^2+y^2+2=0\left(vn\right)\)
Vậy hẹ pt có nghiệm (x;y)=(0;0) ; (2;2)

Gọi số CLB tối đa là x (nguyên dương).
Theo nguyên lý Dirichlet, từ 10 học sinh nào đó luôn có ít nhất \(\left[\dfrac{10+x-1}{x}\right]\) học sinh tham gia cùng 1 CLB
\(\Rightarrow\left[\dfrac{9+x}{x}\right]=3\Rightarrow\left[\dfrac{9}{x}+1\right]=3\)
\(\Rightarrow\left[\dfrac{9}{x}\right]+1=3\Rightarrow\left[\dfrac{9}{x}\right]=2\)
\(\Rightarrow2\le\dfrac{9}{x}< 3\Rightarrow3< x\le\dfrac{9}{2}\)
\(\Rightarrow x=4\)
Khi đó theo nguyên lý Dirichlet luôn tồn tại 1 CLB có ít nhất \(\left[\dfrac{35+4-1}{4}\right]=9\) học sinh

\(2,\\ a,\sqrt{4x-4}+\sqrt{9x-9}-\sqrt{25x-25}=7\left(x\ge1\right)\\ \Leftrightarrow2\sqrt{x-1}+3\sqrt{x-1}-5\sqrt{x-1}=7\\ \Leftrightarrow0\sqrt{x-1}=7\Leftrightarrow x\in\varnothing\\ b,\sqrt{2x^2-3}=4\left(x\le-\dfrac{\sqrt{6}}{2};\dfrac{\sqrt{6}}{2}\le x\right)\\ \Leftrightarrow2x^2-3=16\\ \Leftrightarrow x^2=\dfrac{19}{2}\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{\dfrac{19}{2}}\left(tm\right)\\x=-\sqrt{\dfrac{19}{2}}\left(tm\right)\end{matrix}\right.\)
\(1,\\ A=\sqrt{5+4x}+\sqrt{7-3x}\\ ĐKXĐ:\left\{{}\begin{matrix}5+4x\ge0\\7-3x\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge-\dfrac{5}{4}\\x\le\dfrac{7}{3}\end{matrix}\right.\)

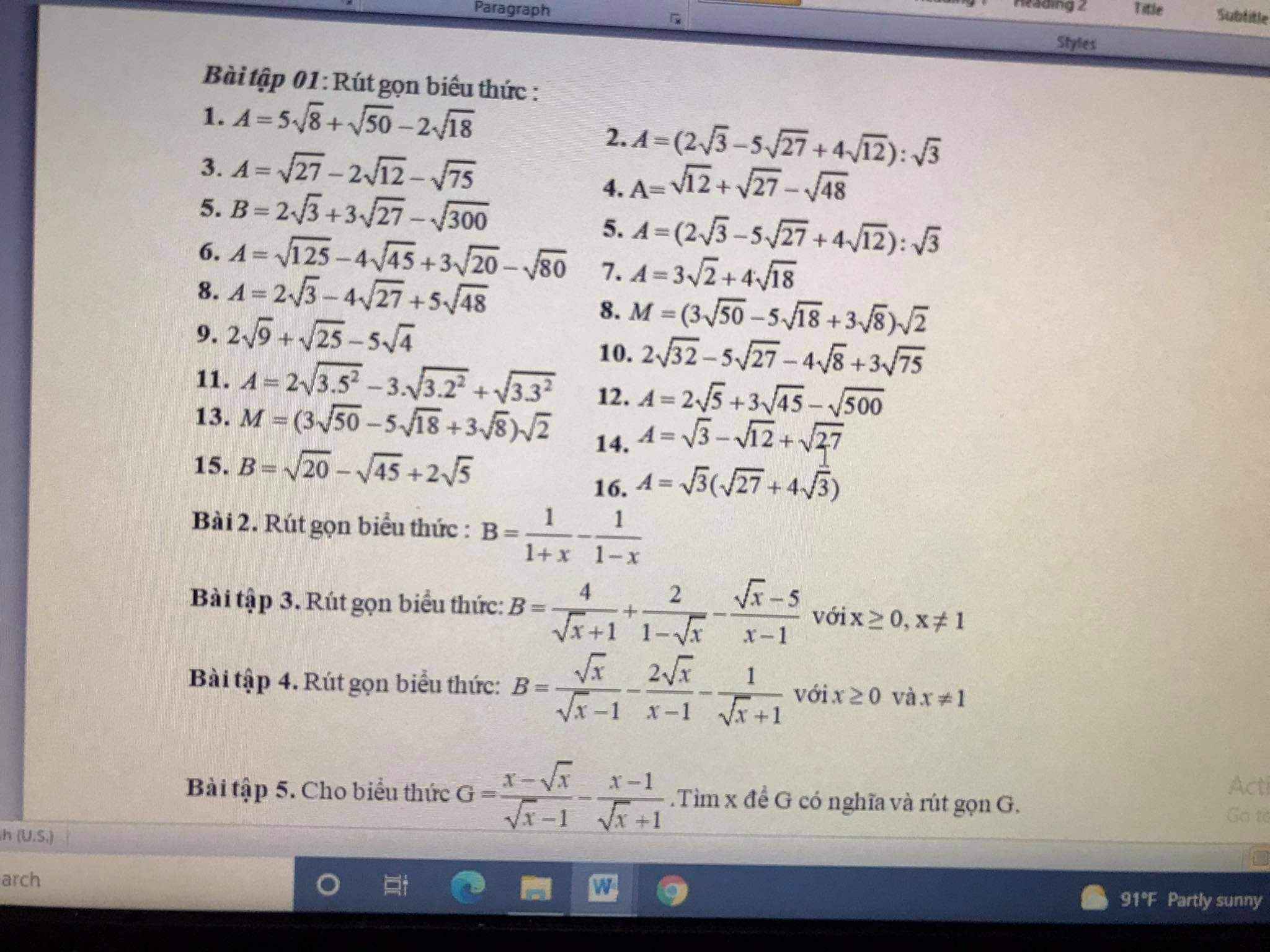
Bài 5:
ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne1\end{matrix}\right.\)
Ta có: \(G=\dfrac{x-\sqrt{x}}{\sqrt{x}-1}-\dfrac{x-1}{\sqrt{x}+1}\)
\(=\sqrt{x}-\sqrt{x}+1\)
=1


A) \(\sqrt{4\left(1-x\right)^2}-6=0\)
\(\sqrt{4\left(1-x\right)^2}=6\)
\(\hept{\begin{cases}4\left(1-x\right)=6\\4\left(1-x\right)=-6\end{cases}}\)
\(\hept{\begin{cases}x=-\frac{1}{2}\\x=\frac{5}{2}\end{cases}}\)
B)\(\sqrt{1-12x+36x^2}=5\)
\(\sqrt{\left(1-6x\right)^2}=5\)
\(\hept{\begin{cases}1-6x=5\\1-6x=-5\end{cases}}\)
\(\hept{\begin{cases}x=-\frac{2}{3}\\x=1\end{cases}}\)

=2/(xy+yz+zx)+2/(x^2+y^2+z^2)+1/xy+yz+zx
>=2(4/(x+y+z)^2)+1/(1/3)>=8+3=11(hình như sai đề nhưng cách làm là đúng rồi)
=2/(xy+yz+zx)+2/(x^2+y^2+z^2)+1/xy+yz+zx
>=2(4/(x+y+z)^2)+1/(1/3)>=8+3=11(hình như sai đề nhưng cách làm là đúng rồi)



bạn có lộn câu không bạn