Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho tam giác không có góc tù , nội tiếp đường tròn , (, cố định, di động trên cung lớn BC). Các tiếp tuyến tại và cắt nhau tại . Từ kẻ đường thẳng song song với , đường thẳng này cắt tại và ( thuộc cung nhỏ ), cắt tại , cắt tại . Chứng minh rằng . Từ đó suy ra là tứ giác nội tiếp.
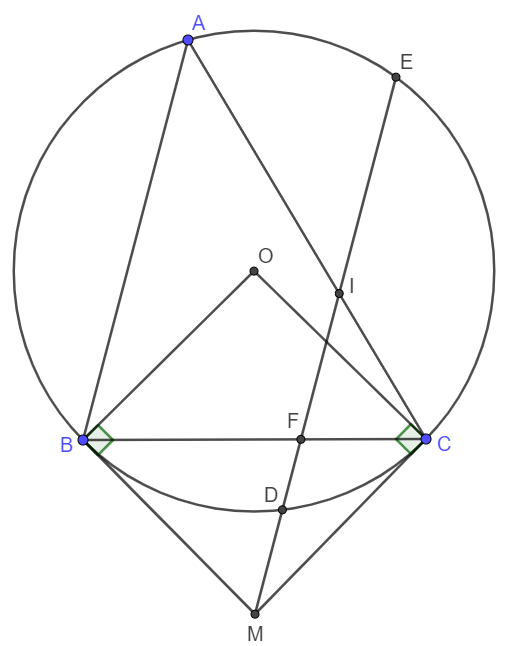
theo gt, ta co:
goc MBC= BAC (cung chan cung BC)
mat khac, ta lai co goc BAC = MIC ( dong vi)
=> goc MBC= MIC
=> tu giac BICM noi tiep

Áp dụng đlí Py - ta - go cho tam giác BAO vuông tại B , ta có :
\(OA^2=OB^2+AB^2\)
\(AB^2=OA^2-OB^2=5^2-3^2=16\)
\(AB^2=16\Rightarrow AB=4cm\)
=> AC = 4cm
Theo tính chất 2tt cắt nhau , ta có :
DB = DM ; EC = EM
=> AD + DE + AE = AB + AC = 4 + 4 = 8
Vậy : chu vi tam giác ADE là : 8cm

c) Gọi T là giao điểm thứ hai của FD với đường tròn (O). Ta c/m EO đi qua T.
Ta có: ^ADM = ^DAC + ^DCA = ^BAC/2 + ^ACB = ^BAD + ^MAB = ^MAD => \(\Delta\)DAM cân tại M => MA=MD
Lại có: MA và MF là 2 tiếp tuyến của (O) nên MA=MF. Do đó: MD=MF => \(\Delta\)MDF cân tại M (đpcm).
Dễ thấy: \(\Delta\)MAB ~ \(\Delta\)MCA (g.g) và \(\Delta\)MFB ~ \(\Delta\)MCF (g.g)
=> \(\frac{MA}{MC}=\frac{MF}{MC}=\frac{AB}{AC}=\frac{BD}{CD}=\frac{FB}{FC}\) => FD là tia phân giác ^BFC (1)
Kẻ tia đối Fy của FB => ^EFy = ^ECB = ^EBC = ^EFC => FE là phân giác ^CFy (2)
Từ (1) và (2) suy ra: FD vuông góc với FE (Vì ^BFC + ^CFy = 1800) hay ^EFT = 900
=> ET là đường kính của (O) => ET trùng với OE => OE đi qua T => ĐPCM.
d) Áp dụng ĐL Ptolemy có tứ giác BFCT nội tiếp có: BF.CT + CF.BT = BC.FT
=> CT.(BF+CF) = BC.FT => \(BF+CF=\frac{BC.FT}{CT}\le\frac{BC.ET}{CT}=\frac{2CK.ET}{CT}=2EC=2BE\)
Dấu "=" xảy ra khi F trùng với E <=> MF vuông góc OE <=> MF // BC => M không nằm trên BC (mâu thuẫn)
=> Không có dấu "=" => BF+CF < 2BE (đpcm).

a: góc CEM+góc CDM=180 độ
=>CEMD nội tiếp
b: góc EDM=góc ECM
góc FDM=góc FBM=góc ABM
=>góc EDF=góc ACM+góc ABM=60 độ

a/
D và E cùng nhìn MC dưới 1 góc vuông -> CDME là tứ giác nội tiếp
b/
CM tương tự ta cũng có tứ giác BDMF là tứ giác nội tiếp
\(\Rightarrow\widehat{MBF}=\widehat{MDF}\) (góc nt cùng chắn cung MF) (1)
Xét tứ giác nt CDME có
\(\widehat{MCE}=\widehat{MDE}\) (góc nt cùng chắn cung MF) (2)
Từ (1) và (2) \(\Rightarrow\widehat{MBF}+\widehat{MCE}=\widehat{MDF}+\widehat{MDE}=\widehat{EDF}\) (3)
Xét \(\Delta ABC\) có
AB=AC (Hai tiếp tuyến cùng xp từ 1 điểm)
=> \(\Delta ABC\) cân tại A \(\Rightarrow\widehat{ABC}=\widehat{ACB}=\dfrac{180^o-\widehat{xAy}}{2}=\dfrac{180^o-60^o}{2}=60^o\)
Ta có
\(sđ\widehat{ABC}=\dfrac{1}{2}sđ\) cung BC => sđ cung BC = 2.sđ \(\widehat{ABC}=2.60^o=120^o\)
=> sđ cung BM + sđ cung CM = sđ cung BC \(=120^o\)
Ta có
\(sđ\widehat{MBF}=\dfrac{1}{2}sđ\) cung BM (góc giữa tiếp tuyến và dây cung)
\(sđ\widehat{MCE}=\dfrac{1}{2}sđ\) cung CM (góc giữa tiếp tuyến và dây cung)
\(\Rightarrow sđ\widehat{MBF}+sđ\widehat{MCE}=sđ\widehat{EDF}=\dfrac{sđcungBM+sđcungCM}{2}=\dfrac{sđcungBC}{2}=\dfrac{120^0}{2}=60^o\)
c/
Xét tg vuông MBF và tg vuông MCD có
\(sđ\widehat{MBF}=\dfrac{1}{2}sđcungBM\) (góc giữa tiếp tuyến và dây cung)
\(sđ\widehat{MCD}=\dfrac{1}{2}sđcungBM\) (góc nt)
\(\Rightarrow\widehat{MBF}=\widehat{MCD}\) => tg MBF đồng dạng với tg MCD
\(\Rightarrow\dfrac{MF}{MD}=\dfrac{MB}{MC}\)
CM tương tự ta cũng có tg vuông MCE đồng dạng với tg vuông MBD
\(\Rightarrow\dfrac{ME}{MD}=\dfrac{MC}{MB}\Rightarrow\dfrac{MD}{ME}=\dfrac{MB}{MC}\)
\(\Rightarrow\dfrac{MF}{MD}=\dfrac{MD}{ME}\Rightarrow MD^2=ME.MF\left(đpcm\right)\)

Theo tính chất của hai tiếp tuyến cắt nhau ta có :
DB = DM
EM = EC
Chu vi của tam giác ADE bằng :
AD + DE + EA = AD + DM + ME + EA
= AD + DB + AE + EC = AB + AC = 2AB
Mà tứ giác ABOC là hình vuông (chứng minh trên) nên:
AB = OB = 2 (cm)
Vậy chu vi của tam giác ADE bằng: 2.2 = 4 (cm)