Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
góc EAH+góc ACB=90 độ
góc EBC+góc ACB=90 độ
=>góc EAH=góc EBC
b: AK cắt EF tại M
AK cắt BC tại N
AH cắt (O) tại K
=>HM//AB và QN//AB
=>HM//QN

Cho tam giác không có góc tù , nội tiếp đường tròn , (, cố định, di động trên cung lớn BC). Các tiếp tuyến tại và cắt nhau tại . Từ kẻ đường thẳng song song với , đường thẳng này cắt tại và ( thuộc cung nhỏ ), cắt tại , cắt tại . Chứng minh rằng . Từ đó suy ra là tứ giác nội tiếp.
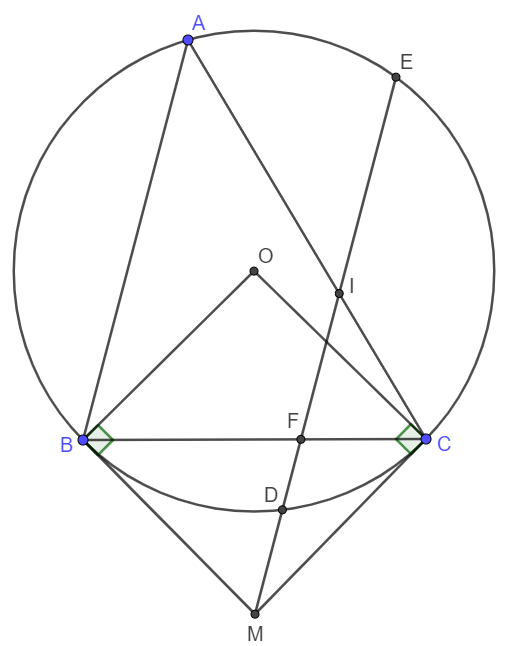
theo gt, ta co:
goc MBC= BAC (cung chan cung BC)
mat khac, ta lai co goc BAC = MIC ( dong vi)
=> goc MBC= MIC
=> tu giac BICM noi tiep

a) vì AD là tia phân giác \(\widehat{BAC}\)
\(\Rightarrow\widehat{BAD}=\widehat{DAC}\)\(\Rightarrow\)D là điểm chính giữa BC
\(\Rightarrow OD\perp BC\)
Mà \(DE\perp OD\)
\(\Rightarrow BC//DE\)
b) Ta có : \(\widehat{DAC}=\widehat{DCI}=\frac{1}{2}sđ\widebat{CD}\)
\(\Rightarrow\widehat{KAD}=\widehat{KCI}\)
suy ra tứ giác ACIK nội tiếp
c) OD cắt BC tại H
Dễ thấy H là trung điểm BC nên HC = \(\frac{BC}{2}=\frac{\sqrt{3}}{2}R\)
Xét \(\Delta OHC\)vuông tại H có :
\(HC=OC.\sin\widehat{HOC}\Rightarrow\sin\widehat{HOC}=\frac{HC}{OC}=\frac{\frac{\sqrt{3}}{2}R}{R}=\frac{\sqrt{3}}{2}\)
\(\Rightarrow\widehat{HOC}=60^o\)
\(\Rightarrow\widehat{BOC}=120^o\)
\(\Rightarrow\widebat{BC}=120^o\)
P/s : câu cuối là tính số đo cung nhỏ BC mà sao có cái theo R. mình ko hiểu. thôi thì bạn cứ xem đi nha.

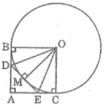
Theo tính chất của hai tiếp tuyến cắt nhau ta có :
DB = DM
EM = EC
Chu vi của tam giác ADE bằng :
AD + DE + EA = AD + DM + ME + EA
= AD + DB + AE + EC = AB + AC = 2AB
Mà tứ giác ABOC là hình vuông (chứng minh trên) nên:
AB = OB = 2 (cm)
Vậy chu vi của tam giác ADE bằng: 2.2 = 4 (cm)

a: Xét (O) có
CM,CA là tiếp tuyến
Do đó: CM=CA và OC là phân giác của \(\widehat{AOM}\)
=>\(\widehat{COM}=\dfrac{1}{2}\cdot\widehat{MOA}\)
Xét (O) có
DM,DB là tiếp tuyến
Do đó: DM=DB và OD là phân giác của \(\widehat{MOB}\)
=>\(\widehat{MOD}=\dfrac{1}{2}\cdot\widehat{MOB}\)
\(\widehat{COD}=\widehat{COM}+\widehat{DOM}\)
\(=\dfrac{1}{2}\cdot\widehat{MOA}+\dfrac{1}{2}\cdot\widehat{MOB}\)
\(=\dfrac{1}{2}\left(\widehat{MOA}+\widehat{MOB}\right)=\dfrac{1}{2}\cdot180^0=90^0\)
CD=CM+MD
mà CM=CA và DM=DB
nên CD=CA+DB
b: Xét ΔOCD vuông tại O có OM là đường cao
nên \(OM^2=CM\cdot MD\)
=>\(AC\cdot BD=R^2\)
c: CM=CA
OM=OA
Do đó: CO là đường trung trực của AM
=>CO\(\perp\)AM tại E
DM=DB
OM=OB
Do đó: OD là đường trung trực của MB
=>OD\(\perp\)MB tại F
Xét tứ giác MEOF có
\(\widehat{MEO}=\widehat{MFO}=\widehat{FOE}=90^0\)
=>MEOF là hình chữ nhật
=>EF=OM=R