Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBMC và ΔDMA có
MB=MD
góc BMC=góc DMA
MC=MA
=>ΔBMC=ΔDMA
=>góc MBC=góc MDA
=>BC//AD
b: Xét tứ giác ABCD có
M là trung điểm chung của AC và BD
=>ABCD là hbh
=>AB=CD
=>CD=CA
=>ΔCAD cân tại C
c: Xét ΔEBD có
EM là trung tuyến
EC=2/3EM
=>C là trọng tâm
=>DC đi qua trung điểm của BE

a: Sửa đề: ΔABC cân tại A
Xét ΔABM và ΔACN có
AB=AC
góc BAM chung
AM=AN
=>ΔABM=ΔACN
=>BM=CN
Xét ΔACB có
BM,Cn là trung tuyến
BM cắt CN tại G
=>G là trọng tâm
=>BG=2/3BM và CG=2/3CN
mà BM=CN
nên BG=CG
b: BG=2/3BM
=>BG=2GM
=>BG=GD
=>G là trung điểm của BD và BD=2BG
CG=2/3CN
=>CG=2GN
=>CG=GE
=>G là trung điểm của CE và CE=2CG
CE=2CG
BD=2BG
mà CG=BG
nên CE=BD
Xét tứ giác BCDE có
G là trung điểm chung của BD và CE
CE=BD
=>BCDE là hình chữ nhật

a: Xét ΔBMC và ΔDMA có
MB=MD
góc BMC=góc DMA
MC=MA
=>ΔBMC=ΔDMA
=>góc MBC=góc MDA
=>BC//AD
b: Xét tứ giác ABCD có
M là trung điểm chung của AC và BD
=>ABCD là hbh
=>AB=CD=CA và AD=BC
b,c: Đề sai rồi bạn

a: Xét ΔABM và ΔCDM có
MA=MC
\(\widehat{AMB}=\widehat{CMD}\)
MB=MD
Do đó: ΔABM=ΔCDM
b: Ta có: ΔABM=ΔCDM
nên \(\widehat{ABM}=\widehat{CDM}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD

a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
b: Xét tứ giác AGCK có
M là trung điểm của đường chéo AC
M là trung điểm của đường chéo GK
Do đó: AGCK là hình bình hành
Suy ra: AG//CK
Ta có: ΔABC cân tại A
mà AH là đường cao ứng với cạnh đáy BC
nên H là trung điểm của BC
Xét ΔBAC có
AH là đường trung tuyến ứng với cạnh BC
BM là đường trung tuyến ứng với cạnh AC
AH cắt BM tại G
Do đó: G là trọng tâm của ΔABC
Suy ra: \(BG=\dfrac{2}{3}BM\)
\(\Leftrightarrow GM=MK=\dfrac{1}{3}BM\)
\(\Leftrightarrow GM+MK=GK=\dfrac{2}{3}BM\)
\(\Leftrightarrow BG=GK\)
hay G là trung điểm của BK

a/
MA=MC (gt); MB=MQ (gt) => ABCQ là hbh (Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường)
=> AQ=BC (cạnh đối hbh) (1)
\(\widehat{ABC}=\widehat{AQC}\) (góc đối hbh) (2)
Ta có BL=BC (cạnh hình vuông) (3)
Ta có
\(\widehat{DBL}+\widehat{ABC}=360^o-\widehat{ABD}-\widehat{LBC}=360^o-90^o-90^o=180^o\left(4\right)\)
\(\widehat{BAQ}+\widehat{AQC}=180^o\) (5)
Xét \(\Delta BDL\) và \(\Delta ABQ\) có
BD=AB (cạnh hình vuông)
Từ (1) và (3) => BL=AQ
Từ (2) (4) (5) => \(\widehat{DBL}=\widehat{BAQ}\)
\(\Rightarrow\Delta BDL=\Delta ABQ\) (c.g.c) => DL=BQ
Câu b xem lại đề bài

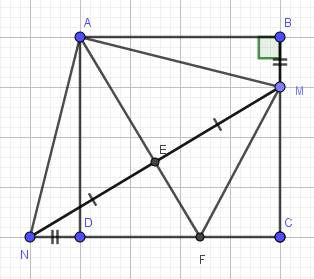
a) Do ABCD là hình vuông (gt)
\(\Rightarrow AB=AD\)
\(\widehat{ABM}=\widehat{ADN}=90^0\)
Xét hai tam giác vuông: \(\Delta ABM\) và \(\Delta ADN\) có:
\(AB=AD\left(cmt\right)\)
\(BM=DN\left(gt\right)\)
\(\Rightarrow\Delta ABM=\Delta ADN\) (hai cạnh góc vuông)
\(\Rightarrow AM=AN\) (hai cạnh tương ứng)
\(\widehat{BAM}=\widehat{DAN}\) (hai góc tương ứng)
Ta có:
\(\widehat{BAM}+\widehat{DAM}=90^0\)
\(\Rightarrow\widehat{DAN}+\widehat{DAM}=90^0\)
\(\Rightarrow\widehat{MAN}=90^0\)
\(\Delta AMN\) có:
\(AM=AN\left(cmt\right)\)
\(\Rightarrow\Delta AMN\) cân tại A
Mà \(\widehat{MAN}=90^0\left(cmt\right)\)
\(\Rightarrow\Delta AMN\) vuông cân tại A
b) Do \(\Delta AMN\) cân tại A
E là trung điểm của MN
\(\Rightarrow AE\) là đường trung tuyến, cũng là đường cao của \(\Delta AMN\)
\(\Rightarrow AE\perp MN\)
\(\Rightarrow EF\perp MN\)
Xét hai tam giác vuông: \(\Delta FEM\) và \(\Delta FEN\) có:
\(EM=EN\left(gt\right)\)
\(EF\) là cạnh chung
\(\Rightarrow\Delta FEM=\Delta FEN\) (hai cạnh góc vuông)
\(\Rightarrow FM=FN\) (hai cạnh tương ứng)
Xét \(\Delta FAN\) và \(\Delta FAM\) có:
\(FA\) là cạnh chung
\(FN=FM\left(cmt\right)\)
\(AN=AM\left(cmt\right)\)
\(\Rightarrow\Delta FAN=\Delta FAM\left(c-c-c\right)\)
b: Xét ΔAMB và ΔCMD có
MA=MC
góc AMB=góc CMD
MB=MD
=>ΔAMB=ΔCMD
c: G là trọng tâm
=>BG=2/3BM=2/3*1/2*BD=1/3*BD