Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔHFA vuông tại F và ΔHDC vuông tại D có
\(\widehat{FHA}=\widehat{DHC}\)(hai góc đối đỉnh)
Do đó: ΔHFA~ΔHDC
=>\(\dfrac{HF}{HD}=\dfrac{HA}{HC}\)
=>\(HF\cdot HC=HD\cdot HA\left(1\right)\)
Xét ΔHFB vuông tại F và ΔHEC vuông tại E có
\(\widehat{FHB}=\widehat{EHC}\)(hai góc đối đỉnh)
Do đó: ΔHFB~ΔHEC
=>\(\dfrac{HF}{HE}=\dfrac{HB}{HC}\)
=>\(HF\cdot HC=HB\cdot HE\left(2\right)\)
Từ (1) và (2) suy ra \(HA\cdot HD=HF\cdot HC=HB\cdot HE\)
c: Xét tứ giác AFHE có \(\widehat{AFH}+\widehat{AEH}=90^0+90^0=180^0\)
nên AFHE là tứ giác nội tiếp
Xét tứ giác BFHD có \(\widehat{BFH}+\widehat{BDH}=90^0+90^0=180^0\)
nên BFHD là tứ giác nội tiếp
Xét tứ giác CEHD có \(\widehat{CEH}+\widehat{CDH}=90^0+90^0=180^0\)
nên CEHD là tứ giác nội tiếp
Ta có: \(\widehat{EFH}=\widehat{EAH}\)(AEHF là tứ giác nội tiếp)
\(\widehat{DFH}=\widehat{DBH}\)(BFHD là tứ giác nội tiếp)
mà \(\widehat{EAH}=\widehat{DBH}\left(=90^0-\widehat{ECB}\right)\)
nên \(\widehat{EFH}=\widehat{DFH}\)
=>FH là phân giác của góc EFD
Ta có: \(\widehat{FEH}=\widehat{FAH}\)(AEHF là tứ giác nội tiếp)
\(\widehat{DEH}=\widehat{DCH}\)(ECDH là tứ giác nội tiếp)
mà \(\widehat{FAH}=\widehat{DCH}\left(=90^0-\widehat{ABD}\right)\)
nên \(\widehat{FEH}=\widehat{DEH}\)
=>EH là phân giác của góc FED
Xét ΔFED có
EH,FH là các đường phân giác
Do đó: H là giao điểm của ba đường phân giác trong ΔFED
Xét ∆AHE và ∆BHD, ta có
<D=<E=90°
<BHD=<EHA ( đối đỉnh)
⟹ ∆AHE ∼∆BHD(g.g)
⟹HA/HB=HE/HD⟹ HA*HD=HB*HE
Nguồn: Lazi.
< Bạn tự vẽ hình nha>
a)Xét ΔABE và ΔACF, ta có:
góc A: chung
góc F=góc E= 90o
Vậy ΔABE ∼ ΔACF (g.g)
b)Xét ΔHEC và ΔHFB là:
góc H: chung
H1=H2(đối đỉnh)
Vậy ΔHEC∼ ΔHFB (g.g)
⇒\(\dfrac{HE}{HF}\)=\(\dfrac{HC}{HB}\)⇔HE.HB=HF.HC
<Mình chỉ biết đến đó thôi>
đó nha bna,Xét tg DHB và tg DCA có: ^HDB=^CDA=90 độ, ^DBH=^DAC ( cùng phụ với hai góc bằng nhau BHD=^AHE)
Do đó: tg HDB đồng dạng tg DCA (g.g)
Suy ra: HD/DC=BD/DA-> bd*dc=dh*da
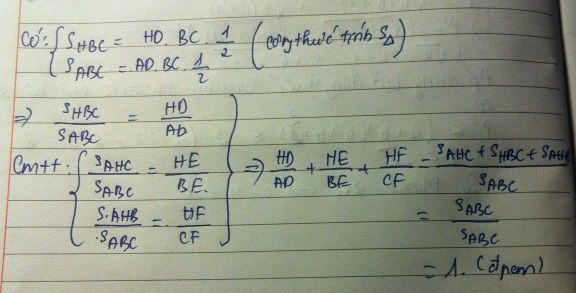
b, HD/HA=SBHC/SABC
HE/BE=SAHC/SABC
HF/CF=SHAB/SABC
HD/HA+HE/BE+HF/CF=SBHC/SABC+SAHC/SABC+SAHB/SABC=1
a: Xét tứ giác BHCK có
M là trung điểm của BC
M là trung điểm của HK
Do đó: BHCK là hình bình hành
Xét ΔHDB VÀ ΔHEA, có:
\(\widehat{BHD}\) = \(\widehat{EHA}\)( đối đỉnh)
\(\widehat{BDH}\) = \(\widehat{HEA}\) = 90°( giả thiết )
Do đó ΔHDB ∞ ΔHEA
➜ \(\dfrac {HD}{HE}\) = \(\dfrac{HB}{HA}\) ➜ HA . HD = HB . HE