Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì H ∈∈ BC nên ta có :
BC = BH + HC => 8 = 3 + HC
=> HC = 8 - 3 => HC = 5 cm
Áp dụng định lý pytago vào :
+) ΔABH ta có: AB^2 = BH^2 + AH^2 => AH^2 = AB^2 - BH^2
=> AH^2 = 562 - 3^2 => AH^2 = 25 - 9
=> AH^2 = 16 => AH = 4cm (do AH > 0cm )
+) ΔAHC có : AC^2 = AH^2 + HC^ 2 => AC ^2 = 4^2 + 5^2
=> AC^2 = 16 + 25 => AC^2 = 41
=> AC = \(\sqrt{41}cm\left(do\right)AC>0cm\)
Vậy AH = 4 cm ; HC = 5 cm ; AC = \(\sqrt{41}\)
Học tốt

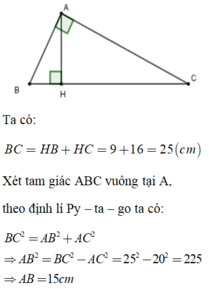
TA CÓ TAM GIÁC ABH VUÔNG TẠI H ;A/D ĐỊNH LÝ PYTAGO TA CÓ
\(AB^2=AH^2+BH^2=>BH^2=AB^2-AH^2\)
=>\(BH^2=15^2-12^2=>BH^2=81=>BH=9'\left(cm\right)\)
=>\(BC=9+16=25\left(cm\right)\)
ta có \(\Delta AHC\) VUÔNG TẠI H A/D ĐỊNHLÝ PYTAGO TA CÓ
\(AC^2=AH^2+HC^2=>AC^2=12^2+16^2\)
=>\(AC^2=400=>AC=20\left(cm\right)\)

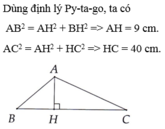
Áp dụng định lý Pi-ta-go vào tam giác vuông ABH vuông tại H ta có:
AB2= BH2 + AH2
<=> 152= 122+ AH2
<=> AH2= 152- 122= 225- 144= 81
<=> AH= 9 (cm)
Tương tự ta có : Áp dụng định lý Pi-ta-go vào tam giác vuông ACH vuông tại H .
AC2= AH2+ HC2
<=> 412= 92+ HC2
<=> HC2= 412- 92= 1681- 81= 1600
<=>HC= 40 (cm)

Tam giác AHC vuông tại H nên : AC^2 = AH^2 + CH^2 = 12^2 + 16^2 = 400
=> AC = 20 (cm)
Tam giác AHB vuông tại H nên : AB^2 = AH^2 + BH^2
=> BH^2 = AB^2 - AH^2 = 13^2 - 12^2 = 25
=> BH = 5 (cm)
=> BC = BH + HC = 5 + 16 = 21 (cm)
Tk mk nha

Xét \(\Delta ABH\)vuông tại H ta có :
\(AB^2+BH^2=AH^2\)(định lí Pitago)
=> \(AH^2=AB^2-BH^2\)
=> \(AH^2=5^2-3^2\)
=> \(AH^2=25-9=16\)
=> \(AH=4\left(cm\right)\)
Ta có : \(BH+HC=BC\)
=> \(3+HC=8\)
=> \(HC=5\left(cm\right)\)
Xét \(\Delta AHC\)vuông tại H ta có :
\(AH^2+HC^2=AC^2\)
=> \(4^2+5^2=AC^2\)
=> \(16+25=AC^2\)
=> \(AC^2=41\)
=> \(AC=\sqrt{41}\)(vì AC > 0)