Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(A\left(x_A;y_A\right);B\left(x_B;y_B\right);C\left(x_C;y_C\right)\).
\(\overrightarrow{MN}\left(1;2\right)\); \(\overrightarrow{BP}\left(-x_B;-4-y_B\right)\).
MN là đường trung bình của tam giác ABC nên: \(\overrightarrow{MN}=\dfrac{1}{2}\overrightarrow{BC}=\overrightarrow{BN}\).
Vì vậy \(\left\{{}\begin{matrix}-x_B=1\\-4-y_B=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_B=-1\\y_B=-6\end{matrix}\right.\)\(\Leftrightarrow B\left(-1;-6\right)\).
\(\overrightarrow{NP}\left(-2;-7\right)\); \(\overrightarrow{AM}\left(1-x_A;1-y_A\right)\).
NP là đường trung bình của tam giác ABC nên:
\(\overrightarrow{NP}=\dfrac{1}{2}\overrightarrow{AB}=\overrightarrow{AM}\).
Vì vậy \(\left\{{}\begin{matrix}1-x_A=-2\\1-y_A=-7\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x_A=3\\y_A=8\end{matrix}\right.\)\(\Rightarrow A\left(3;8\right)\).
Do M là trung điểm của AB nên:
\(\dfrac{x_A+x_B}{2}=x_M\Rightarrow x_B=2x_M-x_A=2.1-3=-1\).
\(\dfrac{y_A+y_B}{2}=y_M\Rightarrow y_B=2y_M-y_A=2.1-8=-6\).
Vậy \(B\left(-1;-6\right)\).
bạn ơi, cách làm của bạn thì ok lắm nhưng theo mình thì có vẻ bạn đang nhầm đề bài á??... ví dụ ở đề bài M là trung điểm của BC nhưng trong hình vẽ của bạn điểm M lại là trung điểm của AB mất rồi!!! Đó là suy nghĩ của mình thoii, nếu như không hợp lý thì mình xin lỗi :))

Tọa độ G là;
\(\left\{{}\begin{matrix}x=\dfrac{4+2+0}{3}=2\\y=\dfrac{0-4-2}{3}=-2\end{matrix}\right.\)
Tọa độ M là:
x=(2+0)/2=1 và y=(-4-2)/2=-3
Tọa độ N là:
x=(4+0)/2=2 và y=(0-2)/2=-1
Tọa độ P là;
x=(4+2)/2=3 và y=(0-4)/2=-2
Tọa độ trọng tâm của tam giác MNP là:
\(\left\{{}\begin{matrix}x=\dfrac{1+2+3}{3}=2\\y=\dfrac{-3-1-2}{3}=-2\end{matrix}\right.\)
=>Tam giác ABC và tam giác MNP có chung trọng tâm

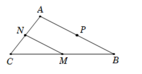
Do M và N lần lượt là trung điểm của BC và AC nên MN là đường trung bình của tam giác AB.

Đáp án B

Theo tích chất đường trung bình trong một tam giác ta có: \(\overrightarrow {PN} = \overrightarrow {BM} = \overrightarrow {MC} \) và \(\overrightarrow {MP} = \overrightarrow {NA} \)
Gọi \(A\left( {{a_1},{a_2}} \right),B\left( {{b_1};{b_2}} \right),C\left( {{c_1};{c_2}} \right)\)
Ta có: \(\overrightarrow {PN} = \left( {2;3} \right)\),\(\overrightarrow {BM} = \left( {1 - {b_1}; - 2 - {b_2}} \right)\), \(\overrightarrow {MC} = \left( {{c_1} - 1;{c_2} + 2} \right)\), \(\overrightarrow {MP} = \left( {5;4} \right)\), \(\overrightarrow {NA} = \left( {{a_1} - 4;{a_2} + 1} \right)\)
Có \(\overrightarrow {PN} = \overrightarrow {BM} \Leftrightarrow \left\{ \begin{array}{l}2 = 1 - {b_1}\\3 = - 2 - {b_2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{b_1} = - 1\\{b_2} = - 5\end{array} \right.\) .Vậy \(B\left( { - 1; - 5} \right)\)
Có \(\overrightarrow {PN} = \overrightarrow {MC} \Leftrightarrow \left\{ \begin{array}{l}2 = {c_1} - 1\\3 = {c_2} + 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{c_1} = 3\\{c_2} = 1\end{array} \right.\) .Vậy \(C\left( {3;1} \right)\)
Có \(\overrightarrow {NA} = \overrightarrow {MP} \Leftrightarrow \left\{ \begin{array}{l}5 = {a_1} - 4\\4 = {a_2} + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{a_1} = 9\\{a_2} = 3\end{array} \right.\) .Vậy \(A\left( {9;3} \right)\)

a: \(\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BC}\)
\(=\overrightarrow{CB}+\overrightarrow{BC}\)
\(=\overrightarrow{0}\)
b: \(\overrightarrow{AM}+\overrightarrow{AP}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)=\dfrac{1}{2}\cdot2\cdot\overrightarrow{AN}=\overrightarrow{AN}\)
Giả sử \(B\left(x;y\right)\).Do \(M\left(2;0\right)\) là trung điểm \(BC\Rightarrow C\left(4-x;-y\right)\).
Do \(N\left(2;3\right)\) là trung điểm \(CA\) \(\Rightarrow A\left(x;6+y\right)\)
Do \(P\left(-1;3\right)\) là trung điểm \(AB\Rightarrow\left\{{}\begin{matrix}x+x=2.\left(-1\right)\\6+y+y=2.3\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}2x=-2\\2y=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-1\\y=0\end{matrix}\right.\\ \Rightarrow B\left(-1;0\right);A\left(-1;6\right);C\left(5;0\right)\).