Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt AB=b, AC=a,AD=d vậy ta CM : 1/c+1/b=\(\sqrt{2}\)/d
Từ D hạ DH vuông AC tại H và DM vuông AB tại M, dễ dàng CM được AHDM là hình vuông. => HD=DM=d.sin45 = \(\frac{d}{\sqrt{2}}\)
Ta có S(ABC) = S(ACD) + S(ABD)
<=> b.c/2 = HD.b/2 + DM.c/2 <=> bc = \(\frac{bd+cd}{\sqrt{2}}\)<=> \(\sqrt{2}\)bc = bd + cd
Chia 2 vế cho b.c.d ta có pt cần CM

\(\frac{1}{b}+\frac{1}{c}=\frac{1}{d}\Leftrightarrow\frac{b+c}{bc}=\frac{1}{d}\Leftrightarrow d=\frac{bc}{b+c}\)
Ta có
\(HD\perp AB;AC\perp AB\) => HD//AC \(\Rightarrow\frac{BD}{BC}=\frac{HD}{AC}=\frac{d}{b}\Rightarrow d=\frac{b.BD}{BC}\) (*)
Xét tg ABC có AD là phân giác của \(\widehat{A}\) nên
\(\frac{BD}{AB}=\frac{CD}{AC}\) (Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy)
\(\Rightarrow\frac{BD}{c}=\frac{CD}{b}=\frac{BD+CD}{b+c}=\frac{BC}{b+c}\Rightarrow BC=\frac{BD.\left(b+c\right)}{c}\) Thay vào (*)
\(d=\frac{b.BD}{\frac{BD.\left(b+c\right)}{c}}=\frac{b.BD.c}{BD.\left(b+c\right)}=\frac{bc}{b+c}\Leftrightarrow\frac{1}{b}+\frac{1}{c}=\frac{1}{d}\left(dpcm\right)\)

a,Ta có \(FM//AD\left(gt\right)\Rightarrow\widehat{EFA}=\widehat{DAB}\left(đvị\right);\widehat{FEA}=\widehat{DAE}\left(slt\right)\)
mà \(\widehat{DAB}=\widehat{DAE}\Rightarrow\widehat{EFA}=\widehat{FEA}\)
\(\Rightarrow\Delta AFE\)cân tại A
xét \(\Delta BMF\left(AD//MF\right)\)Áp dụng định lí ta-let ta có
\(\frac{BF}{AF}=\frac{BM}{DM}\)
b, \(\Delta ABC\)có AD là đường phân giác
\(\Rightarrow\frac{BD}{DC}=\frac{AB}{AC}\Rightarrow\frac{BD}{AB}=\frac{DC}{AC}^{^{\left(1\right)}}\)
Ta có AD//EM => \(\widehat{EMD}=\widehat{ADB};\widehat{ADM}=\widehat{EMC}\left(đvị\right)\)
Xét \(\Delta ECM\)và \(\Delta ACD\)có
\(\widehat{C}:chung \)
\(\widehat{EMC}=\widehat{ADC}\left(cmt\right)\)
\(\Rightarrow\Delta ECM\)VÀ \(\Delta ACD\)đồng dạng (g.g)
\(\Rightarrow\frac{CM}{CE}=\frac{CD}{CA}^{^{\left(2\right)}}\)
Chứng minh tương tự ta có
\(\Delta ABD\)và \(\Delta FAM\)đồng dạng (g.g)
\(\Rightarrow\frac{DB}{AB}=\frac{MB}{BF}^{^{\left(3\right)}}\)
Từ (1)(2)(3) \(\Rightarrow\frac{CM}{CE}=\frac{MB}{BF}\) mà CM=MB (gt) nên CE=BF
p/s: câu c để mình nghĩ tiếp

a) Vì \(BE//AD\) nên \(\widehat {EBA} = \widehat {BAD}\) (cặp góc so le trong) (1)
Vì \(BE//AD\) nên \(\widehat {BEA} = \widehat {DAC}\) (cặp góc đồng vị) (2)
Vì \(AD\) là tia phân giác nên \(\widehat {BAD} = \widehat {DAC}\) (tính chất) (3)
Từ (1); (2); (3) suy ra \(\widehat {EBA} = \widehat {AEB}\) (tính chất bắc cầu)
Xét tam giác \(BAE\) có:
\(\widehat {EBA} = \widehat {AEB}\) (chứng minh trên)
Nên tam giác \(BAE\) cân tại \(A\).
b) Vì \(BE//AD\) nên \(\frac{{BD}}{{DC}} = \frac{{AE}}{{AC}}\).
Mà tam giác \(BAE\) cân tại \(A\) nên \(AE = AB \Rightarrow \frac{{AE}}{{AC}} = \frac{{AB}}{{AC}}\) (định lí Thales)
Do đó, \(\frac{{DB}}{{DC}} = \frac{{AE}}{{AC}} = \frac{{AB}}{{AC}}\) (điều phải chứng minh).
a: AD//BE
=>góc CAD=góc CEB và góc BAD=góc ABE
mà góc CAD=góc BAD
nên góc CEB=góc ABE
=>ΔBAE cân tại A
b: ΔBAE cân tại A
=>AB=AE
=>AB/AC=AE/AC
mà AE/AC=BD/DC(ΔCEB có AD//BE)
nên AB/AC=AE/AC=DB/DC
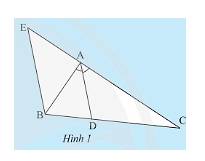
P/s: Hình vẽ chỉ mang tính chất minh họa
Từ D kẻ các đường song song với AC,AB cắt AB,AC lần lượt tại E,F
=> Tứ giác AEDF là hình bình hành
Lại có AD là phân giác góc EAF => Tứ giác AEDF là hình thoi
=> AE = ED = DF = FA
Xét trong tam giác AED cân tại E có góc EAD = 60 độ
=> Tam giác AED đều => AD = DE = DF
Áp dụng định lý Thales ta có:
DE // AC => \(\frac{DE}{AC}=\frac{BD}{BC}\) ; DF // AB => \(\frac{DF}{AB}=\frac{DC}{BC}\)
Cộng vế với vế 2 đẳng trên ta được: \(\frac{DE}{AC}+\frac{DF}{AB}=\frac{BD}{BC}+\frac{DC}{BC}\)
\(\Leftrightarrow\frac{AD}{AC}+\frac{AD}{AB}=1\Rightarrow\frac{1}{AB}+\frac{1}{AC}=\frac{1}{AD}\)
=> đpcm