Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn đáp án B.
x – y = 2 (1) ⇒ a = 1; b = -1; c = 2
A. 2x – 2y = 2 ⇒ a' = 2; b' = -2; c = 2
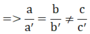⇒ hpt vô nghiệm
B. -2x + 2y + 4 = 0 ⇔ -2x + 2y = - 4 ⇒ a'= -2; b'= 2; c'= -4
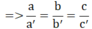⇒ hpt có vô số nghiệm
C. 2y = -2x – 4 ⇔ 2x + 2y = -4 ⇒ a' = 2; b' = 2; c' = -4
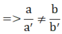⇒ hpt có 1 nghiệm duy nhất
D. y = 2x – 2 ⇔ 2x – y = 2 ⇒ a' = 2; b'= -1
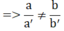⇒ hpt có 1 nghiệm duy nhất
Để hệ phương trình có nghiệm duy nhất thì \(\dfrac{m}{2}\ne\dfrac{2}{-4}=-\dfrac{1}{2}\)
=>\(m\ne-1\)
\(\left\{{}\begin{matrix}mx+2y=1\\2x-4y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2mx+4y=2\\2x-4y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\left(2m+2\right)=5\\2x-4y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{2m+2}\\4y=2x-3=\dfrac{10}{2m+2}-3=\dfrac{10-6m-6}{2m+2}=\dfrac{-6m+4}{2m+2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{2m+2}\\y=\dfrac{-6m+4}{8m+8}=\dfrac{-3m+2}{4m+4}\end{matrix}\right.\)
x-3y=7/2
=>\(\dfrac{5}{2m+2}-\dfrac{3\cdot\left(-3m+2\right)}{4m+4}=\dfrac{7}{2}\)
=>\(\dfrac{10+3\left(3m-2\right)}{4m+4}=\dfrac{7}{2}\)
=>\(\dfrac{10+9m-6}{4m+4}=\dfrac{7}{2}\)
=>\(\dfrac{9m+4}{4m+4}=\dfrac{7}{2}\)
=>7(4m+4)=2(9m+4)
=>28m+28=18m+8
=>10m=-20
=>m=-2(nhận)
`a,x-3y=2`
`<=>x=3y+2` ta thế vào phương trình trên:
`2(3y+2)+my=-5`
`<=>6y+4+my=-5`
`<=>y(m+6)=-9`
HPT có nghiệm duy nhất:
`<=>m+6 ne 0<=>m ne -6`
HPT vô số nghiệm
`<=>m+6=0,-6=0` vô lý `=>x in {cancel0}`
HPT vô nghiệm
`<=>m+6=0,-6 ne 0<=>m ne -6`
b,HPT có nghiệm duy nhất
`<=>m ne -6`(câu a)
`=>y=-9/(m+6)`
`<=>x=3y+2`
`<=>x=(-27+2m+12)/(m+6)`
`<=>x=(-15+2m)/(m+6)`
`x+2y=1`
`<=>(2m-15)/(m+6)+(-18)/(m+6)=1`
`<=>(2m-33)/(m+6)=1`
`2m-33=m+6`
`<=>m=39(TM)`
Vậy `m=39` thì HPT có nghiệm duy nhất `x+2y=1`
b)Ta có: \(\left\{{}\begin{matrix}2x+my=-5\\x-3y=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2+3y\\2\left(2+3y\right)+my=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2+3y\\6y+my+4=-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3y+2\\y\left(m+6\right)=-9\end{matrix}\right.\)
Khi \(m\ne6\) thì \(y=-\dfrac{9}{m+6}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3y+2\\y=\dfrac{-9}{m+6}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\cdot\dfrac{-9}{m+6}+2\\y=-\dfrac{9}{m+6}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{-27}{m+6}+\dfrac{2m+12}{m+6}=\dfrac{2m-15}{m+6}\\y=\dfrac{-9}{m+6}\end{matrix}\right.\)
Để hệ phương trình có nghiệm duy nhất thỏa mãn x+2y=1 thì \(\dfrac{2m-15}{m+6}+\dfrac{-18}{m+6}=1\)
\(\Leftrightarrow2m-33=m+6\)
\(\Leftrightarrow2m-m=6+33\)
hay m=39
Vậy: Khi m=39 thì hệ phương trình có nghiệm duy nhất thỏa mãn x+2y=1
Ta có: 3x – 2y = 5 ⇔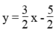 
Để được một hệ có vô số nghiệm thì cần thêm một phương trình bậc nhất hai ẩn có hệ số góc bằng 3/2 và tung độ gốc bằng - 5/2 .
Chẳng hạn: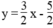 
⇔ 6x – 4y = 10
Khi đó ta có hệ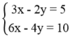 
có vô số nghiệm.
Đáp án là B
x –2y = 2 ⇒ a = 1; b = -2; c = 2
A. 2x – 2y = 2 ⇒ a' = 2; b' = -2; c = 2
B. -2x + 4y - 4 = 0 ⇔ -2x + 4y = 4 ⇒ a' = -2; b' = 4; c' = 4
C. 2y = -2x – 4 ⇔ 2x + 2y = -4 ⇒ a' = 2; b'= 2; c' = -4
D. y = 2x – 4 ⇔ -2x + y = -4 ⇒ a' = -2; b' = 1; c' = -4