Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

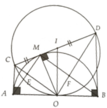
a, Dễ thấy A M B ^ = 90 0 hay E M F ^ = 90 0 tiếp tuyến CM,CA
=> OC ⊥ AM => O E M ^ = 90 0 Tương tự => O F M ^ = 90 0
Chứng minh được ∆CAO = ∆CMO => A O C ^ = M O C ^
=> OC là tia phân giác của A M O ^
Tương tự OD là tia phân giác của B O M ^ suy ra OC ⊥ OD <=> C O D ^
b, Do ∆AOM cân tại O nên OE là đường phân giác đồng thời là đường cao
=> O E M ^ = 90 0 chứng minh tương tự O F M ^ = 90 0
Vậy MEOF là hình chữ nhật
c, Gọi I là trung điểm CD thì I là tâm đường tròn đường kính CD và IO=IC=ID. Có ABDC là hình thang vuông tại A và B nên IO//AC//BD và IO vuông góc với AB. Do đó AB là tiếp tuyến của đường tròn đường kính CD.

a) Ta có: CD là tiếp tuyến của (O) tại M (gt)
=> CM \(\perp\)MO => \(\widehat{CMO}=90^o\)
AC là tiếp tuyến của (O) tại A (gt)
=> \(AC\perp AO\Rightarrow\widehat{CAO}=90^o\)
Xét tứ giác OACM có: \(\widehat{CMO}+\widehat{CAO}=90^o+90^o=180^o\)
=> OACM nội tiếp (1)
Chứng minh Tương tự : OBDM nội tiếp (2)
b) M thuộc (O), AB là đường kính
=> \(\widehat{EMF}=\widehat{AMB}=90^o\)( góc chắn nửa đường tròn) (3)
Ta có: \(CO\perp AM\)( tự chứng minh bài toán quen thuộc )
=> \(\widehat{OEM}=90^o\)(4)
Tương tự \(\widehat{OFM}=90^o\)(5)
Từ 3, 4, 5 => Tứ giác OEFM là hình chữ nhật (tứ giác có 3 góc vuông ) (6)
c) Ta có: \(\widehat{IOK}=\widehat{EOF}=90^o\)( theo 6)
Mặt khác: I là trung điểm OC, tam giác CMO vuông tại M
=> CM=IC=IO=> tam giác CIM cân => \(\widehat{IMC}=\widehat{MCI}\)
mà \(\widehat{MCI}=\widehat{MCO}=\widehat{MAO}\)( từ 1)
=> \(\widehat{IMC}=\widehat{MAO}\), chứng minh tương tự \(\widehat{KMD}=\widehat{MBO}\)
=> \(\widehat{IMC}+\widehat{KMD}=\widehat{MAO}+\widehat{MBO}=90^o\)Vì tam giác AMB vuông tại M
=> \(\widehat{IMK}=90^o\)
Xét tứ giác OIMK có: \(\widehat{IMK}+\widehat{IOK}=180^o\)
=> OIMK nội tiếp
d) IK là đường trung bình của tam giác COD =>IK=1/2CD và OH=1/2 OM (Với H là giao điểm OM và IK=> OH vuông IF)
=> \(S_{\Delta IOK}=\frac{1}{4}S_{\Delta OCD}\)
Tam giác IKM= tam giác IKO (c.c.c)
=> \(S_{\Delta IOK}=S_{\Delta IMK}\)
=> \(S_{IMKO}=S_{\Delta IOK}+S_{\Delta IMK}=\frac{1}{2}S_{\Delta COD}\)
Ta lại có: tam giác COM= tam giác COA , tam giác MOD=tam giác BOD
=> \(S_{COD}=S_{\Delta COM}+S_{\Delta MOD}=\frac{1}{2}S_{CAMO}+\frac{1}{2}S_{MDBO}=\frac{1}{2}S_{ACDB}\)
=> \(S_{IMKO}=\frac{1}{4}S_{ACDB}=\frac{1}{4}.\frac{1}{2}\left(AC+DB\right).AB\)=10 (cm)vì ACDB là hình thang vuông với đáy AC, DB và đường cao AB

Bạn tự vẽ hình nhé :
1.Vì CM,CA là tiếp tuyến của (O)
\(\Rightarrow CM\perp OM,CA\perp OA\)
\(\Rightarrow CAOM\)nội tiếp đường tròn đường kính OC
Tương tự DMOB nội tiếp đường tròn đường kính OD
2 . Vì CM,CA là tiếp tuyến của (O)
\(\Rightarrow CM=CA,OC\) là phân giác \(\widehat{AOM}\)
Tương tự DM = DB , OD là phân giác ^BOM
Mà \(\widehat{AOM}+\widehat{MOB}=180^0\)
\(\Rightarrow OC\perp OD\)
Lại có ; \(OM\perp CD\Rightarrow CM.DM=OM^2\Rightarrow CM.DM=R^2\)
Mà : \(CM=CA,DM=DB\Rightarrow AC.BD=R^2\Rightarrow AC.3R=R^2\Rightarrow AC=\frac{R}{3}\)
\(\Rightarrow S_{ABCD}=\frac{1}{2}AB\left(BD+CA\right)=\frac{1}{2}.2R.\left(3R+\frac{R}{3}\right)=\frac{10R^2}{3}\)
3.Vì CM,CA là tiếp tuyến của (O)
\(\Rightarrow CO\perp AM=E\) là trung điểm AM
Tương tự \(OD\perp BM=F\) là trung điểm BM
\(\Rightarrow MN\) là đường trung bình \(\Delta ABC\Rightarrow EF//MN\)
Mà \(OE\perp ME,OF\perp MF,MN\perp ON\)
\(\Rightarrow M,E,N,O,F\in\) đường tròn đường kính OM
\(\Rightarrow EFNO\) nội tiếp
\(\Rightarrow\widehat{EFO}+\widehat{ENO}=180^0\)
Mà \(\widehat{NEF}+\widehat{ENO}=180^0\) ( EF // AB => EF//NO )
\(\Rightarrow EFON\) là hình thang cân

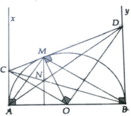
a, Từ CA, CM là tiếp tuyến của (O) chứng minh được A,C,M,O ∈ đường tròn bán kính O C 2
b, Chứng minh OC,BM cùng vuông góc với AM . từ đó suy ra OC//BM
c, S A C D B = A C + B D A B 2 = A D . A B 2
=> S A C D B nhỏ nhất khi CD có độ dài nhỏ nhất
Hay M nằm chính giữa cung AB
d, Từ tính chất hai giao tuyến => AC = CM và BM=MD, kết hợp với AC//BD
ta chứng minh được C N N B = C M M D => MN//BD => MN ⊥ AB

Bạn tự vẽ hình nha!
c) Các tam giác ACM và BDM cân tại C và D; CO là phân giác góc ACM; DO là phân giác góc BDM => Các đường phân giác này cũng là đường cao => CO vuông góc với AM tại E và DO vuông góc với BM tại F => g. OEM = OFM = 90o.
Mặt khác g.AMB =90o(Góc nội tiếp chắn nửa đường tròn) => Từ giác OEMF là hình chữ nhật => I là trung điểm của OM => IO = OM/2 = R/2 (Không đổi)
Do đó khi M di chuyển thì trung điểm I của EF luôn cách O một khoảng không đổi R/2 => Quỹ tích trung điểm I của EF là nửa đường tròn tâm O bán kính R/2 cùng phía với nửa đường trón tâm O đường kính AB.
Bạn tự vẽ hình nha!
c) Các tam giácACM và BDM cân tại C và D; CO là phân giác góc ACM; DO là phân giác góc BDM => Các đường phân giác này cũng là đường cao => CO vuông góc với AM tại E và DO vuông góc với BM tại F => g. OEM = OFM = 90o.
Mặt khác g.AMB =90o(Góc nội tiếp chắn nửa đường tròn) => Từ giác OEMF là hình chữ nhật => I là trung điểm của OM => IO = OM/2 = R/2 (Không đổi)
Do đó khi M di chuyển thì trung điểm I của EF luôn cách O một khoảng không đổi R/2 => Quỹ tích trung điểm I của EF là nửa đường tròn tâm O bán kính R/2 cùng phía với nửa đường trón tâm O đường kính AB.
Ban cm tứ gác MEOF là hình chữ nhật, có EF là dg chéo nên trung điểm của EF là trung điểm của OM. Sr OI bằng R/2. I thuộc cung tròn (O, R/2). phần đảo và kết luận bạn tự làm nhé.