Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
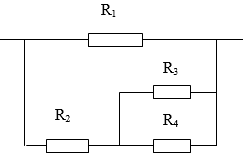
Sơ đồ mạch: R1 // [R2 nt (R3 // R4)]
\(R_{34}=\dfrac{R_3\cdot R_4}{R_3+R_4}=\dfrac{6\cdot6}{6+6}=3\left(\text{Ω}\right)\)
\(R_{234}=R_2+R_{34}=9+3=12\left(\text{Ω}\right)\)
\(R_{tđ}=\dfrac{R_1\cdot R_{234}}{R_1+R_{234}}=\dfrac{12\cdot12}{12+12}=6\left(\text{Ω}\right)\)
theo mạch điện như hình vẽ
\(=>\left(R1ntR3\right)//R2]ntR4\)
do đó \(=>Rtd=R4+\dfrac{\left(R1+R3\right)R2}{R1+R3+R2}\)
\(=6+\dfrac{\left(12+6\right)9}{12+6+9}=12\left(om\right)\)
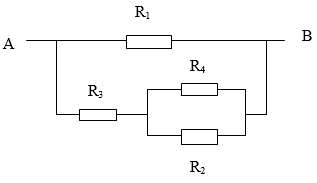
Sơ đồ mạch: R1 // [R3 nt (R2 // R4)]
\(R_{24}=\dfrac{R_2\cdot R_4}{R_2+R_4}=\dfrac{5\cdot10}{5+10}=\dfrac{10}{3}\left(\text{Ω}\right)\)
\(R_{234}=R_3+R_{24}=5+\dfrac{10}{3}=\dfrac{25}{3}\left(\text{Ω}\right)\)
\(R_{AB}=\dfrac{R_1\cdot R_{234}}{R_1+R_{234}}=\dfrac{10\cdot\dfrac{25}{3}}{10+\dfrac{25}{3}}=\dfrac{50}{11}\left(\text{Ω}\right)\)
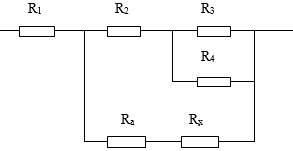
Sơ đồ mạch: R1 nt {[R2 nt (R3 // R4)] // (Ra nt Rx)}
\(R_{34}=\dfrac{R_3\cdot R_4}{R_3+R_4}=\dfrac{12\cdot12}{12+12}=6\left(\text{Ω}\right)\)
\(R_{234}=R_2+R_{34}=4+6=10\left(\text{Ω}\right)\)
\(R_{ax}=R_a+R_x=1+4=5\left(\text{Ω}\right)\)
\(R_{234ax}=\dfrac{R_{234}\cdot R_{ax}}{R_{234}+R_{ax}}=\dfrac{10\cdot5}{10+5}=\dfrac{10}{3}\left(\text{Ω}\right)\)
\(R_{tđ}=R_1+R_{234ax}=10+\dfrac{10}{3}=\dfrac{40}{3}\left(\text{Ω}\right)\)
không đổi; điện trở của dây dẫn và khoá không đáng kể.
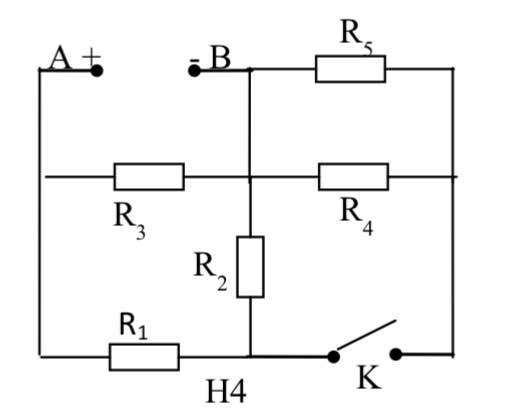
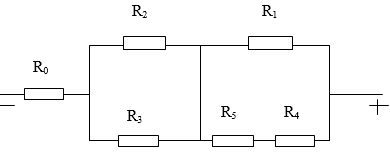
\(\text{Sơ đồ mạch: [R1 // (R4 nt R5)] nt (R2 // R3) nt R0 }\)
\(R_{4,5}=R_4+R_5=3\left(\text{Ω}\right)\)
\(R_{145}=\dfrac{R_1\cdot R_{45}}{R_1+R_{45}}=\dfrac{1\cdot3}{1+4}=0.75\left(\text{Ω}\right)\)
\(R_{23}=\dfrac{R_2\cdot R_3}{R_2+R_3}=\dfrac{2\cdot6}{2+6}=1.5\left(\text{Ω}\right)\)
Điện trở tương đương của mạch là
\(R_{tđ}=R_0+R_{23}+R_{145}=0.5+1.5+0.75=2.75\left(\text{Ω}\right)\)
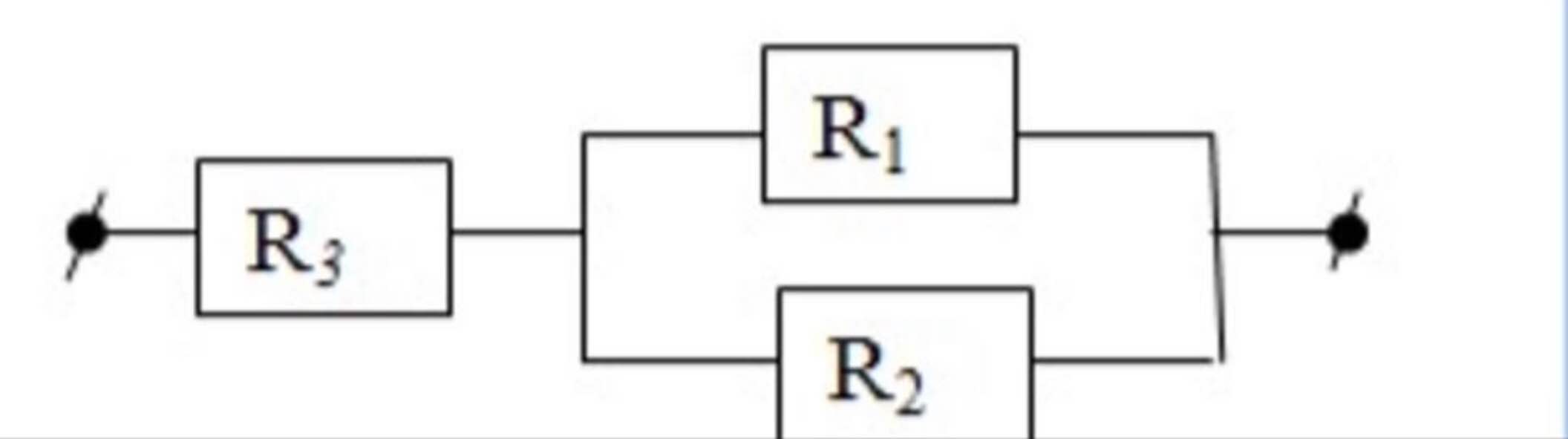
Sơ đồ mạch: R1 // [(R2 // R3) nt R4]
Điện trở tương đương là :
\(R_{23}=\dfrac{R_2\cdot R_3}{R_2+R_3}=\dfrac{4\cdot4}{4+4}=2\left(\text{Ω }\right)\)
\(R_{234}=R_{23}+R_4=6\left(\text{Ω }\right)\)
\(R_{AB}=\dfrac{R_1\cdot R_{234}}{R_1+R_{234}}=\dfrac{3\cdot6}{3+6}=2\left(\text{Ω }\right)\)
Hay