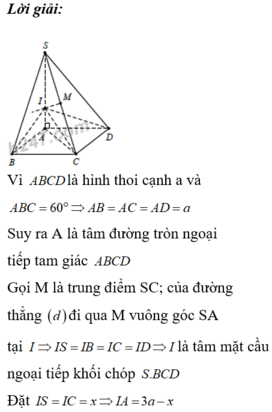
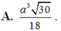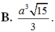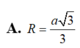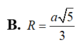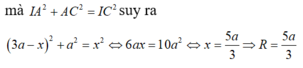Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là B
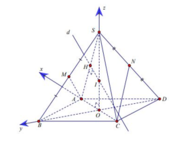
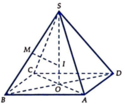
Chọn hệ trục tọa độ Oxyz như hình vẽ, ta có:
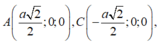
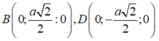
Đặt SO = x > 0. => S (0;0; x).
M , N lần lượt là trung điểm của SB và SD nên:
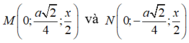
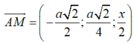
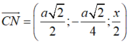
Theo giả thiết: AM ⊥CN
![]()
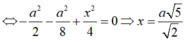
SO là trục đường tròn ngoại tiếp mặt đáy.
Gọi H là trung điểm SA . Qua H dựng đường trung trực d của SA, I= d ∩ SO .
=> Mặt cầu ngoại tiếp khối chóp S .ABCD có tâm I , bán kính R = SI.
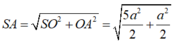
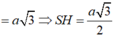
∆ SHI đồng dạng với ∆ SOA

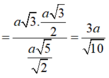
Vậy bán kính mặt cầu ngoại tiếp khối chóp S ABCD . là R= 3 a 10

Đáp án B
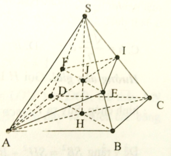
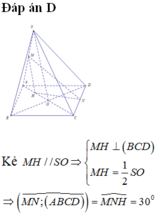
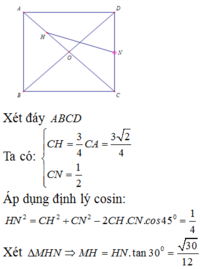
Do các cạnh bên bằng nhau nên hình chiếu của S lên (ABCD) phải trùng với tâm H của hình vuông ABCD.
Dễ thấy I là trung điểm của SC, vì BD ⊥ SC, nên BD//(P). Do đó EF // BD. Để ý rằng EF đi qua trọng tâm J của tam giác SDB.
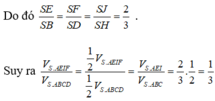

Đáp án A
Phương pháp:
Sử dụng phương pháp tọa độ hóa.
Cách giải:
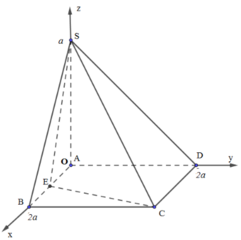
Gắn hệ trục tọa độ như hình vẽ.
Trong đó, B(2a;0;0), C(2a;2a;0), E(a;0;0), S(0;0;a)
Gọi I(x0;y0;z0) là tâm của mặt cầu ngoại tiếp hình chóp S.BEC. Khi đó, IS2 = IB2 = IC2 = IE2
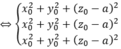
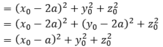
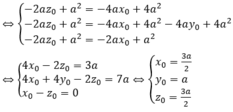
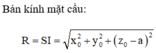
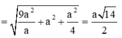
![]()