Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi O là giao điểm AC, BD=> O là trung điểm BC
=> Q là trọng tâm tam giác ABC \(\Rightarrow BQ=\frac{2}{3}BO=\frac{1}{3}BD\)
Lần lượt kẻ QK và OH vuông góc BC \(\Rightarrow\frac{QK}{OH}=\frac{BQ}{BO}=\frac{2}{3}\)(định lí Ta-lét)
Ta có: \(S_{BQM}=\frac{1}{2}.QK.BM\)
\(S_{OBC}=\frac{1}{2}.OH.BC=\frac{1}{2}.\left(\frac{3}{2}QK\right).2BM=3\left(\frac{1}{2}QK.BM\right)=3S_{BQM}\)
Lại có:\(S_{OBC}=\frac{1}{2}S_{BCD}=\frac{1}{4}S_{ABCD}=\frac{1}{4}\)
\(\Rightarrow S_{BQM}=\frac{1}{3}S_{OBC}=\frac{1}{12}\)
\(\Leftrightarrow S_{MQDC}=S_{BCD}-S_{BQM}=\frac{1}{2}-\frac{1}{12}=\frac{5}{12}\)

Dễ thấy SABCD = 2SADC (1)
Gọi O là giao điểm của AC và BD thì O là trung điểm của AC.
Tam giác ADC và tam giác CMD có chung đường cao kẻ từ C nên cho ta :\(\frac{S_{ADC}}{S_{CMD}}=\frac{AD}{MD}=2\)hay SADC = 2SCMD (2)
Tương tự : \(\frac{S_{CMD}}{S_{DME}}=\frac{CM}{ME}=3\)( vì E là trọng tâm của tam giác ADC ) hay SCMD = 3SDME (3)
Từ (1) (2) (3) suy ra SABCD = 12SDME = 12 m2

Gọi I là trung điểm của AD, K là giao điểm của CI và BD. Kẻ ME ^ BD tại E, CF ^ BD tại F.
Có B N = 1 3 B D , E M = 1 2 C F S B M N = 1 2 E M . B N = 1 2 . 1 2 C F . 1 3 B D = 1 6 S B C D = 1 12 S ⇒ S M N D C = 1 2 S − 1 12 S = 5 12 S
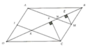

Gọi O là giao điểm AC, BD \(\Rightarrow\) O là trung điểm BC
\(\Rightarrow\) Q là trọng tâm tam giác ABC \(\Rightarrow BQ=\dfrac{2}{3}BO=\dfrac{1}{3}BD\)
Lần lượt kẻ QK và OH vuông góc BC \(\Rightarrow\dfrac{QK}{OH}=\dfrac{BQ}{BO}=\dfrac{2}{3}\) (talet)
Ta có \(S_{BQM}=\dfrac{1}{2}QK.BM\)
\(S_{OBC}=\dfrac{1}{2}OH.BC=\dfrac{1}{2}\left(\dfrac{3}{2}QK\right).2BM=3\left(\dfrac{1}{2}QK.BM\right)=3S_{BQM}\)
Lại có \(S_{OBC}=\dfrac{1}{2}S_{BCD}=\dfrac{1}{4}S_{ABCD}=\dfrac{1}{4}\)
\(\Rightarrow S_{BQM}=\dfrac{1}{3}S_{OBC}=\dfrac{1}{12}\)
\(\Rightarrow S_{MQDC}=S_{BCD}-S_{BQM}=\dfrac{1}{2}-\dfrac{1}{12}=\dfrac{5}{12}\)