TD
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
21 tháng 8 2018
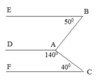
D A B ^ = 360 0 − 140 0 + 90 0 = 130 0
a) D A C ^ + A C F ^ = 140 0 + 40 0 = 180 0
Suy ra AD//CF( vì có cặp góc trong cùng phía bù nhau).
b) D A B ^ + A B E ^ = 130 0 + 50 0 = 180 0
Suy ra AD//BE( vì có cặp góc trong cùng phía bù nhau)
2 tháng 8 2020
c, có ^DAB = ^FAC = 90
^DAB + ^BAC = ^DAC
^FAC + ^BAC = ^FAB
=> ^DAC = ^FAB
xét tg DAC và tg BAF có : AD = AB (gt) và AF = AC (Gt)
=> tg DAC = tg BAF (C-g-c)
=> BF = DC (đn)
TP
2
BED =
2 tháng 7 2023
a: Xét ΔBED vuông tại E và ΔCFD vuông tại F có
DB=DC
góc BDE=góc CDF
=>ΔBED=ΔCFD
b: Xét tứ giác BECF có
BE//CF
BE=CF
=>BECF là hbh
=>CE//BF
6 tháng 9 2020
ban tu ve hinh nha
Ta có : Góc DAB = góc CAE = 90 độ => góc DAB + góc BAC = góc CAE + góc BAc
hay góc DAC = góc EAB
Xét tam giác ADC và tam giác ABE có :
AD = AB ; AC = AE ; góc DAC = góc EAB
=> tam giác ADC = tam giác ABE => DC = BE
Vì tam giác ADC = tam giác ABE nên góc AEB = góc ACD
mà góc AKE = góc BKC (đối đỉnh) , góc AKE + góc AEB = 90 độ
=> góc BKC + góc AEB = 90 độ hay góc BKC + góc ACD = 90 độ
=> góc DC vuông góc BE
HH
26 tháng 6 2018
Giải:
a) Vẽ tia đối của AD là AO
Ta có:
\(\widehat{DAC}+\widehat{CAO}=180^0\) (Hai góc kề bù)
\(\Leftrightarrow140^0+\widehat{CAO}=180^0\)
\(\Leftrightarrow\widehat{CAO}=40^0\)
\(\Leftrightarrow\widehat{CAO}=\widehat{C}\left(=40^0\right)\)
\(\Leftrightarrow AD//CF\) (Vì có hai góc so le trong bằng nhau)
b) Ta có:
\(\widehat{CAO}+\widehat{BAO}=\widehat{BAC}\)
\(\Leftrightarrow40^0+\widehat{BAO}=90^0\)
\(\Leftrightarrow\widehat{BAO}=50^0\)
\(\Leftrightarrow\widehat{BAO}=\widehat{B}\left(=50^0\right)\)
\(\Leftrightarrow AD//BE\) (Vì có hai góc so le trong bằng nhau)
Vậy ...
Câu a chứng minh theo hai góc trong cung phía bù nhau cũng được