Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn có thể giúp mk giải hộ bài này được ko ạ, mk ko bt làm ntn cho đúng, mong bạn giải giúp mk ạ, mk cảm ơn
Cho △ABC. Dựng ra phía ngoài △ABC, các tam giác ABD và ACE vuông cân tại A, kẻ AH ⊥ BC. Đường thẳng AH cắt DE tại M. Vẽ DI và EK vuông góc với AH. Chứng minh
a, DI = EK = AH
b, M là trung điểm của DE

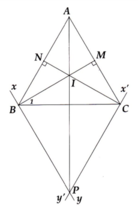
Bạn có thể tham khảo tại đây: Chứng minh BM^2+CN^2 không phụ thuộc vào vị trí của xy biết tam giác ABC vuông cân tại A - Phạm Phú Lộc Nữ
Chúc bn học tốt!

a) Ta có: \(\widehat{BAM}+90^0+\widehat{CAN}=180^o\)
\(\Rightarrow\widehat{BAM}+\widehat{CAN}=90^0\) (1)
Lại có: \(\widehat{ACN}+\widehat{CAN}=90^0\)(tính chất của tam giác vuông) (2)
Từ (1) và (2), suy ra: \(\widehat{BAM}=\widehat{ACN}\)
Xét \(\Delta BAM\perp M\) và \(\Delta CAN\perp N\), ta có:
BA = AC (gt)
\(\widehat{BAM}=\widehat{ACN}\left(cmt\right)\)
\(\Rightarrow\Delta BMA=\Delta CNA\) (cạnh huyền - góc nhọn)
b) Vì \(\Delta BMA=\Delta CNA\) (theo câu a)
Nên BM = AN (2 cạnh tương ứng) (3)
và MA = NC ( 2 cạnh tương ứng) (4)
Ta có: MA + AN = MN (5)
Nên thay (3), (4) vào (5) ta được BM + CN = MN (đpcm)
Chúc you học tốt nhé!!!!~~~~![]()

a, ^NAC + ^BAC + ^MAB = 180 (kb)
^BAC = 90
=> ^NAC + ^MAB = 90
^NAC + ^NCA = 90
=> ^NCA = ^MAB
xét tam giác CNA và tam giác AMB có : AB = AC do tam giác ABC vc (gt)
^CNA = ^AMB = 90
=> tam giác CNA = tam giác AMB (ch-gn)
b, tam giác CNA = tam giác AMB (câu a)
=> NA = BM (đn) và CN = AM (đn)
có : NA + MA = MN
=> BM + CN = MN
c, NC = AM (câu b) => NC^2 = AM^2
xét tam giác MB vuông tại M => BM^2 + AM^2 = AB^2 (pytago)
=> BM^2 + NC^2 = AB^2
mà AB không phụ thuộc vào xy
=> BM^2 + CN^2 không phụ thuộc vào xy