Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, ^NAC + ^BAC + ^MAB = 180 (kb)
^BAC = 90
=> ^NAC + ^MAB = 90
^NAC + ^NCA = 90
=> ^NCA = ^MAB
xét tam giác CNA và tam giác AMB có : AB = AC do tam giác ABC vc (gt)
^CNA = ^AMB = 90
=> tam giác CNA = tam giác AMB (ch-gn)
b, tam giác CNA = tam giác AMB (câu a)
=> NA = BM (đn) và CN = AM (đn)
có : NA + MA = MN
=> BM + CN = MN
c, NC = AM (câu b) => NC^2 = AM^2
xét tam giác MB vuông tại M => BM^2 + AM^2 = AB^2 (pytago)
=> BM^2 + NC^2 = AB^2
mà AB không phụ thuộc vào xy
=> BM^2 + CN^2 không phụ thuộc vào xy

a) Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC(ΔABC cân tại A)
\(\widehat{BAH}\) chung
Do đó: ΔAHB=ΔAKC(cạnh huyền-góc nhọn)
Suy ra: AH=AK(hai cạnh tương ứng)

a) Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC(ΔABC cân tại A)
\(\widehat{BAH}\) chung
Do đó: ΔAHB=ΔAKC(cạnh huyền-góc nhọn)
Suy ra: AH=AK(hai cạnh tương ứng)

a: Xét ΔABC có DE//BC
nên AD/AB=AE/AC
mà AB=AC
nên AD=AE
hay ΔADE cân tại A
b: Xét ΔMBD vuông tại M và ΔNCE vuông tại N có
BD=CE
\(\widehat{BDM}=\widehat{CEN}\)
Do đó: ΔMBD=ΔNCE
c: Xét ΔDBC và ΔECB có
DB=EC
\(\widehat{DBC}=\widehat{ECB}\)
BC chung
Do đó: ΔDBC=ΔECB
Suy ra: \(\widehat{ICB}=\widehat{IBC}\)
hay ΔIBC cân tại I
d: Ta có: IB=IC
nên I nằm trên đường trung trực của BC(1)
Ta có: AB=AC
nên A nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AI là đường trung trực của BC
Ta có: ΔABC cân tại A
mà AI là đường trung trực
nên AI là tia phân giác của góc BAC

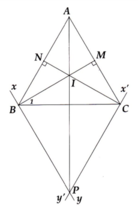
bn ơi chỉ hộ mik câu d vs
Bạn có thể tham khảo tại đây: Chứng minh BM^2+CN^2 không phụ thuộc vào vị trí của xy biết tam giác ABC vuông cân tại A - Phạm Phú Lộc Nữ
Chúc bn học tốt!