Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \({u_{n + 1}} = 3 - 4\left( {n + 1} \right) = 3 - 4n - 4 = - 1 - 4n\)
Xét hiệu: \({u_{n + 1}} - {u_n} = \left( { - 1 - 4n} \right) - \left( {3 - 4n} \right) = - 1 - 4n - 3 + 4n = - 4\)
Vậy dãy số là cấp số cộng có công sai \(d = - 4\).
b) Ta có: \({u_{n + 1}} = \frac{{n + 1}}{2} - 4 = \frac{n}{2} + \frac{1}{2} - 4 = \frac{n}{2} - \frac{7}{2}\)
Xét hiệu: \({u_{n + 1}} - {u_n} = \left( {\frac{n}{2} - \frac{7}{2}} \right) - \left( {\frac{n}{2} - 4} \right) = \frac{n}{2} - \frac{7}{2} - \frac{n}{2} + 4 = \frac{1}{2}\)
Vậy dãy số là cấp số cộng có công sai \(d = \frac{1}{2}\).
c) Ta có: \({u_1} = {5^1} = 5;{u_2} = {5^2} = 25;{u_3} = {5^3} = 125\)
Vì \({u_2} - {u_1} = 20;{u_3} - {u_2} = 100\) nên dãy số không là cấp số cộng.
d) Ta có: \({u_{n + 1}} = \frac{{9 - 5\left( {n + 1} \right)}}{3} = \frac{{9 - 5n - 5}}{3} = \frac{{4 - 5n}}{{3}}\)
Xét hiệu: \({u_{n + 1}} - {u_n} = \frac{{4 - 5n}}{3} - \frac{{9 - 5n}}{3} = \frac{{\left( {4 - 5n} \right) - \left( {9 - 5n} \right)}}{3} = \frac{{4 - 5n - 9 + 5n}}{3} = - \frac{5}{3}\)
Vậy dãy số là cấp số cộng có công sai \(d = - \frac{5}{3}\).

Trong dãy có 3 cấp số nhân:
\(u_n=4\sqrt{5}.\sqrt{5}^{n-1}\) là CSN với \(\left\{{}\begin{matrix}u_1=4\sqrt{5}\\q=\sqrt{5}\end{matrix}\right.\)
\(v_n=-36.\left(-3\right)^{n-1}\) là CSN với \(\left\{{}\begin{matrix}u_1=-36\\q=-3\end{matrix}\right.\)
\(a_n=-4.4^{n-1}\) là CSN với \(\left\{{}\begin{matrix}u_1=-4\\q=4\end{matrix}\right.\)

\(\lim\left(1+\dfrac{-1}{2^n}\right)=1+0=1\Rightarrow a=1\)
\(\lim\left(\dfrac{n^5}{n^4-2n^3+1}-n\right)=\lim\left(\dfrac{n^5-n\left(n^4-2n^3+1\right)}{n^4-2n^3+1}\right)\)
\(=\lim\left(\dfrac{2n^4-n}{n^4-2n^3+1}\right)=\lim\left(\dfrac{2-\dfrac{1}{n^3}}{1-\dfrac{2}{n}+\dfrac{1}{n^4}}\right)=2\)
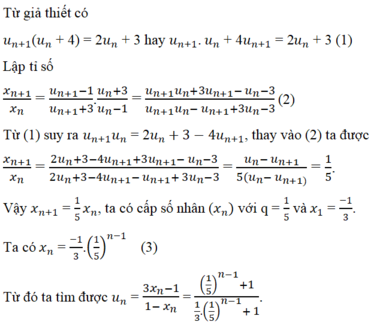
Chọn C
1. u n = 3 n + 1 2. u n = 4 − 5 n
3. u n = 2 n + 3 5 4. u n = n + 1 n
* Xét dãy số: u n = 3 n + 1
Ta có:
u n + 1 − u n = 3 ( n + 1 ) + 1 − 3 n − 1 = 3
Dãy số này là cấp số cộng có công sai d= 3.
* Xét dãy số u n = 4 − 5 n .
Ta có:
u n + 1 − u n = 4 − 5 ( n + 1 ) − ( 4 − 5 n ) = − 5
Dãy số này là cấp số cộng có công sai d = -5
* Xét dãy số u n = 2 n + 3 5
Ta có:
u n + 1 − u n = 2 ( n + 1 ) + 3 5 − 2 n + 3 5 = 2 5 .
Dãy (un) là cấp số cộng có công sai d = 2 5
* Xét dãy số u n = n + 1 n
Ta có:
u n + 1 − u n = n + 1 + 1 n + 1 − n + 1 n = ( n + 2 ) . n − ( n + 1 ) 2 n . ( n + 1 ) = − 1 n ( n + 1 ) ⇒ ( u n )
không là cấp số cộng