Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x | 2 | 4 | 5 | -4 | -1,2 | -24 |
y | -6 | -3 | -2,4 | 3 | 10 | 0,5 |
Vì x và y là hai đại lượng tỉ lệ nghịch, có x1y1 = 2.(-6) = -12 nên ta có công thức \(y = \dfrac{{ - 12}}{x}\).

Lời giải:
Vì $x,y$ là 2 đại lượng tỉ lệ nghịch nên tích của chúng không đổi. Theo giá trị trong bảng thì $xy=2(-6)=-12$ (đây chính là công thức mô tả mối quan hệ phụ thuộc của x,y.
Ta có bảng:
| x | 2 | 4 | 5 | -4 | -1,2 | -24 |
| y | -6 | -3 | -2,4 | 3 | 10 | 0,5 |

Ta thấy: \(\dfrac{{0,5}}{{2,5}} = \dfrac{1}{5} = \dfrac{{1,5}}{{7,5}} = \dfrac{2}{{10}} = \dfrac{{2,5}}{{12,5}}\) nên x và y là 2 đại lượng tỉ lệ thuận.
Công thức liên hệ: \(x = \dfrac{1}{5}.y\) (hay y = 5.x)

| x | X1 = 3 | X2 = 4 | X3 = 5 | X4 = 6 |
| y | Y1 = 6 | Y2 = 8 | Y3 = 10 | Y4 = 12 |

Vì x và y là hai đại lượng tỉ lệ nghịch nên xy = a (với a là một số khác 0).
Khi x = 2, y = 15 ⇒ a = xy = 30
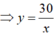
Vì x và y là hai đại lượng tỉ lệ nghịch nên:
x1.y1 = x2.y2 = x3. y3 = x4.y4 = 30.
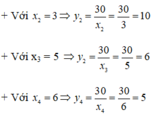
Kết quả như sau:
| x1 = 2 | x2 = 3 | x3 = 5 | x4 = 6 |
| y1 = 15 | y2 = 10 | y3 = 6 | y4 = 5 |
| x1y1 = 30 | x2y2 = 30 | x3y3 = 30 | x4y4 = 30 |

a) Giả sử y tỉ lệ thuận với x theo hệ số tỉ lệ a nên y = a.x nên \(x = \dfrac{y}{a}\)
y tỉ lệ thuận với z theo hệ số tỉ lệ b nên y = b.z
Do đó, \(x = \dfrac{y}{a} = \dfrac{{b.z}}{a} = \dfrac{b}{a}.z\)( \(\dfrac{b}{a}\) là hằng số vì a,b là các hằng số)
Vậy x tỉ lệ thuận với z và hệ số tỉ lệ là \(\dfrac{b}{a}\)
b) Giả sử y tỉ lệ thuận với x theo hệ số tỉ lệ a nên y = a.x nên \(x = \dfrac{y}{a}\)
y tỉ lệ nghịch với z theo hệ số tỉ lệ b nên y = \(\dfrac{b}{z}\)
Do đó, \(x = \dfrac{y}{a} = \dfrac{{\dfrac{b}{z}}}{a} = \dfrac{b}{z}:a = \dfrac{b}{z}.\dfrac{1}{a} = \dfrac{{\dfrac{b}{a}}}{z}\)( \(\dfrac{b}{a}\) là hằng số vì a,b là các hằng số)
Vậy x tỉ lệ nghịch với z và hệ số tỉ lệ là \(\dfrac{b}{a}\)
c) Giả sử y tỉ lệ nghịch với x theo hệ số tỉ lệ a nên y = \(\dfrac{a}{x}\) nên x = \(\dfrac{a}{y}\)
y tỉ lệ nghịch với z theo hệ số tỉ lệ b nên y = \(\dfrac{b}{z}\)
Do đó, \(x = \dfrac{a}{y} = \dfrac{a}{{\dfrac{b}{z}}} = a:\dfrac{b}{z} = a.\dfrac{z}{b} = \dfrac{a}{b}.z\)( \(\dfrac{a}{b}\) là hằng số vì a,b là các hằng số)
Vậy x tỉ lệ thuận với z và hệ số tỉ lệ là \(\dfrac{a}{b}\)

cho x và y là hai đại lượng tỉ lệ thuận, biết rằng hai giá trị bất kì x1,x2 của x có tổng bằng 1, hai giá trị tương ứng y1,y2 của y có tổng bằng 5
a, hãy biểu diễn y theo x
b, tính giá trị của x khi y=-4 , y= -1 và 1 phần 2
c, giá trị của y khi x=-4, x=0,5
ht
cho x và y là hai đại lượng tỉ lệ thuận, biết rằng hai giá trị bất kì x1,x2 của x có tổng bằng 1, hai giá trị tương ứng y1,y2 của y có tổng bằng 5
a, hãy biểu diễn y theo x
b, tính giá trị của x khi y=-4 , y= -1 và 1 phần 2

xy=2
=>y=2/x
y=5z
=>2/x=5z
=>xz=2/5
Vậy: x và z tỉ lệ nghịch theo hệ số tỉ lệ 2/5

Vì x và y là hai đại lượng tỉ lệ thuận, có \(\dfrac{{{y_1}}}{{{x_1}}} = \dfrac{{ - 6}}{2} = - 3\) nên ta có công thức liên hệ \(y = -3. x\)
x
2
4
5
-3
-6
-0,5
y
-6
-12
-15
9
18
1,5