Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔOKB vuông tại K và ΔOHC vuông tại H co
góc KOB=góc HOC
=>ΔOKB đồng dạng với ΔOHC
d: góc BKC=góc BHC=90 độ
=>BKHC nộitiếp
=>góc AKH=góc ACB
=>ΔAKH đồng dạng với ΔACB
=>\(\dfrac{S_{AKH}}{S_{ACB}}=\left(\dfrac{AK}{AC}\right)^2=\dfrac{1}{4}\)
=>\(S_{ABC}=32\left(cm^2\right)\)

+ Xét hai tam giác vuông ABH và ACK có
^BAC chung
AB=AC (tam giác ABC cân tại A)
^ABH=^ACK (cùng phụ với ^ABC)
=> Tam giác ABH=tam giác ACK (g.c.g) => BH=CK
+ Ta có AI là đường cao của t/g ABC (trong 1 tam giác 3 đường cao đồng quy)
=> AI là phân giác ^BAC (Trong tam giác cân đường cao đồng thời là đường phân giác của góc ở đỉnh)
+ Do t/g ABH=t/g ACK => AK=AH mà AB=AC=AK+BK=AH+CH => BK=CH (*)
Do AK=AH => Tam giác AKH cân tại A => ^AKH=^AHK=(180-^BAC):2 (1)
Ta có ^ABC=^ACB=(180-^BAC):2 (2)
=> Từ (1) và (2) ^ABC=^AKH => BC//KH (Hai góc đồng vị băng nhau) (**)
=> Từ (8) và (**) => Tứ giác BKHC là hình thang cân

a: Xét ΔIMB vuông tại M và ΔIKC vuông tại K có
góc MIB=góc KIC
=>ΔIMB đồng dạng vơi ΔIKC
=>IM/IK=IB/IC
=>IM*IC=IB*IK
b: Xét ΔIMA vuông tạiM và ΔIEC vuông tại E có
góc MIA=góc EIC
=>ΔIMA đồng dạng với ΔIEC
=>IM/IE=IA/IC
=>IM*IC=IA*IE
c: Xét ΔAKI vuông tại K và ΔAEC vuông tại E có
góc KAI chung
=>ΔAKI đồng dạng với ΔAEC
=>AK/AE=AI/AC
=>AK*AC=AE*AI
d: Xet ΔAKB vuông tại K và ΔAMC vuông tại M có
góc KAB chung
=>ΔAKB đồng dạng với ΔAMC
=>AK/AM=AB/AC
=>AK*AC=AM*AB

a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
\(\widehat{BAH}\) chung
Do đó: ΔABH\(\sim\)ΔACK
b: Xét ΔKEB vuông tại K và ΔHEC vuông tại H có
\(\widehat{KEB}=\widehat{HEC}\)
DO đó: ΔKEB\(\sim\)ΔHEC
Suy ra: EK/EH=EB/EC
hay \(\dfrac{EK}{EB}=\dfrac{EH}{EC}\)
c: Xét ΔAKH và ΔACB có
AK/AC=AH/AB
góc A chung
Do đó: ΔAKH\(\sim\)ΔACB
Suy ra: \(\widehat{AKH}=\widehat{ACB}\)

a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
\(\widehat{BAH}\) chung
Do đó: ΔABH\(\sim\)ΔACK
b: Xét ΔKEB vuông tại K và ΔHEC vuông tại H có
\(\widehat{KEB}=\widehat{HEC}\)
DO đó: ΔKEB\(\sim\)ΔHEC
Suy ra: EK/EH=EB/EC
hay \(\dfrac{EK}{EB}=\dfrac{EH}{EC}\)
c: Xét ΔAKH và ΔACB có
AK/AC=AH/AB
góc A chung
Do đó: ΔAKH\(\sim\)ΔACB
Suy ra: \(\widehat{AKH}=\widehat{ACB}\)

a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
góc A chung
=>ΔAEB đồng dạng với ΔAFC
=>AE/AF=AB/AC
=>AE*AC=AB*AF và AE/AB=AF/AC
b: Xét ΔAEF và ΔABC có
AE/AB=AF/AC
góc A chung
=>ΔAEF đồng dạng với ΔABC

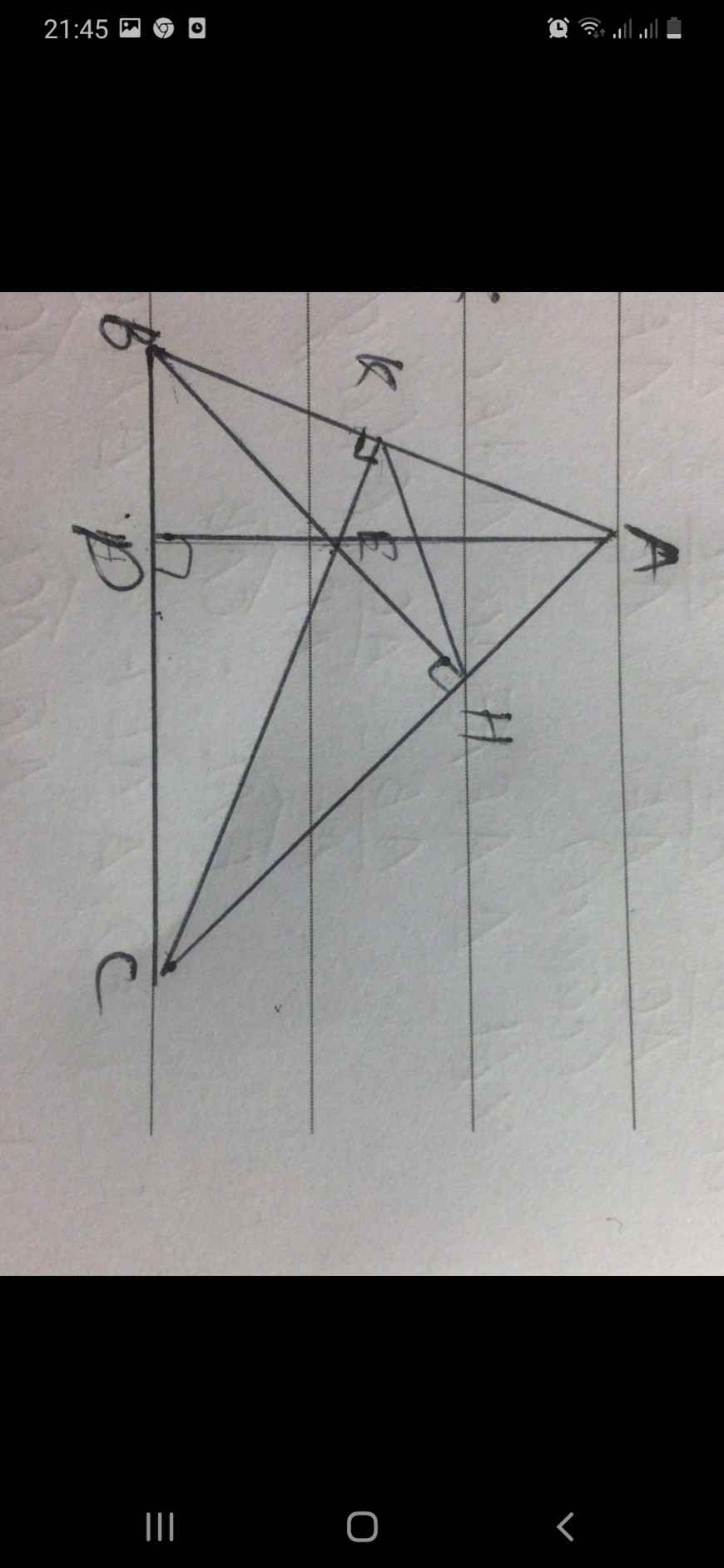

a) Xét ∆KIB và ∆HIC:
\(\widehat{IKB}=\widehat{IHC}=90^o\)
\(\widehat{KIB}=\widehat{HIC}\) (2 góc đối đỉnh)
=> ∆KIB~∆HIC (g.g)
=> \(\dfrac{IB}{IK}=\dfrac{IC}{IH}\)
<=> \(IB.IH=IC.IK\)
b) Theo câu a: ∆KIB~∆HIC
=> \(\dfrac{IK}{IH}=\dfrac{IB}{IC}\)
Xét ∆IBC và ∆IKH:
\(\widehat{BIC}=\widehat{KIH}\) (2 góc đối đỉnh)
\(\dfrac{IK}{IH}=\dfrac{IB}{IC}\) (cmt)
=> ∆IBC~∆IKH
a) Xét ΔKIB vuông tại K và ΔHIC vuông tại H có
\(\widehat{KIB}=\widehat{HIC}\)(hai góc đối đỉnh)
Do đó: ΔKIB\(\sim\)ΔHIC(g-g)
Suy ra: \(\dfrac{IK}{IH}=\dfrac{IB}{IC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(IB\cdot IH=IC\cdot IK\)(đpcm)