Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi n➝(a,b) là VTPT của Đường thẳng d ; A(1,2) ϵ d
--> PTTQ:
(d): a(x-1)+b(y-2)=0
--> ax+by-a-2b=0
d cách đều B,C nên
d(B,d)=d(C,d)
Rồi cứ thế thay công thức rồi tìm đc mối quan hệ a,b. Sau đó thay vào pt đường thẳng d là đc
Minh cũng nghĩ vậy mà thấy phương pháp trên mạng làm khác quá

Giả sử đường thẳng \(\Delta\) cần tìm có phương trình dạng :
\(ax+by+a-3b=0,a^2+b^2\ne0\)
Khi đó :
\(d\left(A;\Delta\right)=\frac{\left|a+2b+a-3b\right|}{\sqrt{a^2+b^2}}=\frac{\left|2a-b\right|}{\sqrt{a^2+b^2}}\)
\(d\left(B;\Delta\right)=\frac{\left|3a+4b+a-3b\right|}{\sqrt{a^2+b^2}}=\frac{\left|4a+b\right|}{\sqrt{a^2+b^2}}\)
Do \(\Delta\) cách đều A, B nên \(d\left(A;\Delta\right)=d\left(B;\Delta\right)\) hay :
\(\frac{\left|2a-b\right|}{\sqrt{a^2+b^2}}=\frac{\left|4a+b\right|}{\sqrt{a^2+b^2}}\)\(\Leftrightarrow\left|2a-b\right|=\left|4a+b\right|\)
\(\Leftrightarrow\begin{cases}a=-b\\a=0\end{cases}\)
- Nếu a=0 thì do \(a^2+b^2\ne0\) nên \(b\ne0\) tùy ý. Do đó, có thể chọn b =1 và ta được \(\Delta_1:y-3=0\)
- Nếu a=-b thì do \(a^2+b^2\ne0\) nên \(b\ne0\) tùy ý. Do đó, có thể chọn a = 1, b=-1 và ta được \(\Delta_2:x-y+4=0\)
Vậy qua C có 2 đường thẳng \(\Delta_1:y-3=0\) và \(\Delta_2:x-y+4=0\) thỏa mãn yêu cầu đề bài
Đường thẳng \(\Delta\) cách đều 2 điểm A, B khi và chỉ khi hoặc \(\Delta\) song song với AB hoặc \(\Delta\) đi qua trung điểm đoạn AB
- Nếu \(\Delta\) // AB thì \(\Delta\) nhận vec tơ \(\overrightarrow{AB}=\left(2;2\right)=2\left(1;1\right)\) làm vec tơ chỉ phương, suy ra nếu có vec tơ pháp tuyến \(\overrightarrow{n}=\left(1;-1\right)\). Vậy \(\Delta:x-y+4=0\)
- Nếu \(\Delta\) đi qua trung điểm M(2;3) của đoạn AB thì \(\Delta\) nhận vec tơ \(\overrightarrow{CM}=\left(3;0\right)=3\left(1;0\right)\) làm vec tơ chỉ phương, suy ra nếu có vec tơ pháp tuyến \(\overrightarrow{m}=\left(0;1\right)\). Vậy \(\Delta:y-3=0\)
àm vec tơ chỉ phương, suy ra nếu có vec tơ pháp tuyến \(\overrightarrow{m}=\left(0;1\right)\). Vậy \(\Delta:y-3=0\)
\(\Delta\) đi qua trung điểm M(2;3) của đoạn AB thì nhận vec tơ \(\overrightarrow{CM}=\left(3;0\right)=3\left(1;0\right)\)

5:
Gọi (d): y=ax+b là phương trình cần tìm
Theo đề, ta có hệ:
3a+b=-1 và 2a+b=3
=>a=-4 và b=11
=>y=-4x+11
4:
vecto BC=(1;-1)
=>AH có VTPT là (1;-1)
Phương trình AH là:
1(x-1)+(-1)(y+3)=0
=>x-1-y-3=0
=>x-y-4=0

d cách đều MN khi nó thỏa mãn 1 trong 2 trường hợp: d song song MN hoặc d đi qua trung điểm MN
TH1: d song song MN
\(\overrightarrow{MN}=\left(3;-4\right)\Rightarrow d\) nhận (4;3) là 1 vtpt
Phương trình d:
\(4\left(x+2\right)+3\left(y-3\right)=0\Leftrightarrow4x+3y-1=0\)
TH2: d đi qua trung điểm MN
Gọi P là trung điểm MN \(\Rightarrow P\left(\dfrac{1}{2};-1\right)\Rightarrow\overrightarrow{AP}=\left(\dfrac{5}{2};-4\right)=\dfrac{1}{2}\left(5;-8\right)\)
\(\Rightarrow d\) nhận (8;5) là 1 vtpt
Phương trình d:
\(8\left(x+2\right)+5\left(y-3\right)=0\Leftrightarrow8x+5y+1=0\)
Có 2 đường thẳng d thỏa mãn: \(\left[{}\begin{matrix}4x+3y-1=0\\8x+5y+1=0\end{matrix}\right.\)

Gọi \(\Delta \) là đường thẳng đi qua B và có vecto pháp tuyến là \(\overrightarrow n = \left( {a;b} \right)\)
Vậy phương trình \(\Delta \) là: \(a\left( {x + 1} \right) + b\left( {y - 2} \right) = 0 \Leftrightarrow {\rm{a}}x + by + \left( {a - 2b} \right) = 0\)
Ta có: \(d\left( {A,\Delta } \right) = d\left( {C,\Delta } \right) \Leftrightarrow \frac{{\left| {3a + 2b} \right|}}{{\sqrt {{a^2} + {b^2}} }} = \frac{{\left| {4a - 3b} \right|}}{{\sqrt {{a^2} + {b^2}} }} \Leftrightarrow \left[ \begin{array}{l}3a + 2b = 4a - 3b\\3a + 2b = - 4a + 3b\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a = 5b\left( 1 \right)\\7a = b\left( 2 \right)\end{array} \right.\)
Từ (1) ta có thể chọn được 1 vecto pháp tuyến là: \(\overrightarrow n = \left( {5;1} \right)\). Vậy phương trình đường thẳng \(\Delta \)là: \(5x + y + 3 = 0\)
Từ (2) ta có thể chọn được 1 vecto pháp tuyến là: \(\overrightarrow n = \left( {1;7} \right)\). Vậy phương trình đường thẳng \(\Delta \)là: \(x + 7y - 13 = 0\)

a.
Gọi phương trình đường tròn (C) có dạng:
\(x^2+y^2-ax-by+c=0\)
Do A;B;C thuộc (C) nên: \(\left\{{}\begin{matrix}0+16-0.a-4b+c=0\\9+16-3a-4b+c=0\\9+0-3a-0.b+c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-4b+c=-16\\-3a-4b+c=-25\\-3a+c=-9\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=3\\b=4\\c=0\end{matrix}\right.\)
Hay pt (C) có dạng: \(x^2+y^2-3x-4y=0\)
b.
Đường tròn (C) tiếp xúc (d) nên có bán kính \(R=d\left(C;d\right)=\dfrac{\left|3.3+0.4-5\right|}{\sqrt{3^2+4^2}}=\dfrac{4}{5}\)
Phương trình: \(\left(x-3\right)^2+y^2=\dfrac{16}{25}\)

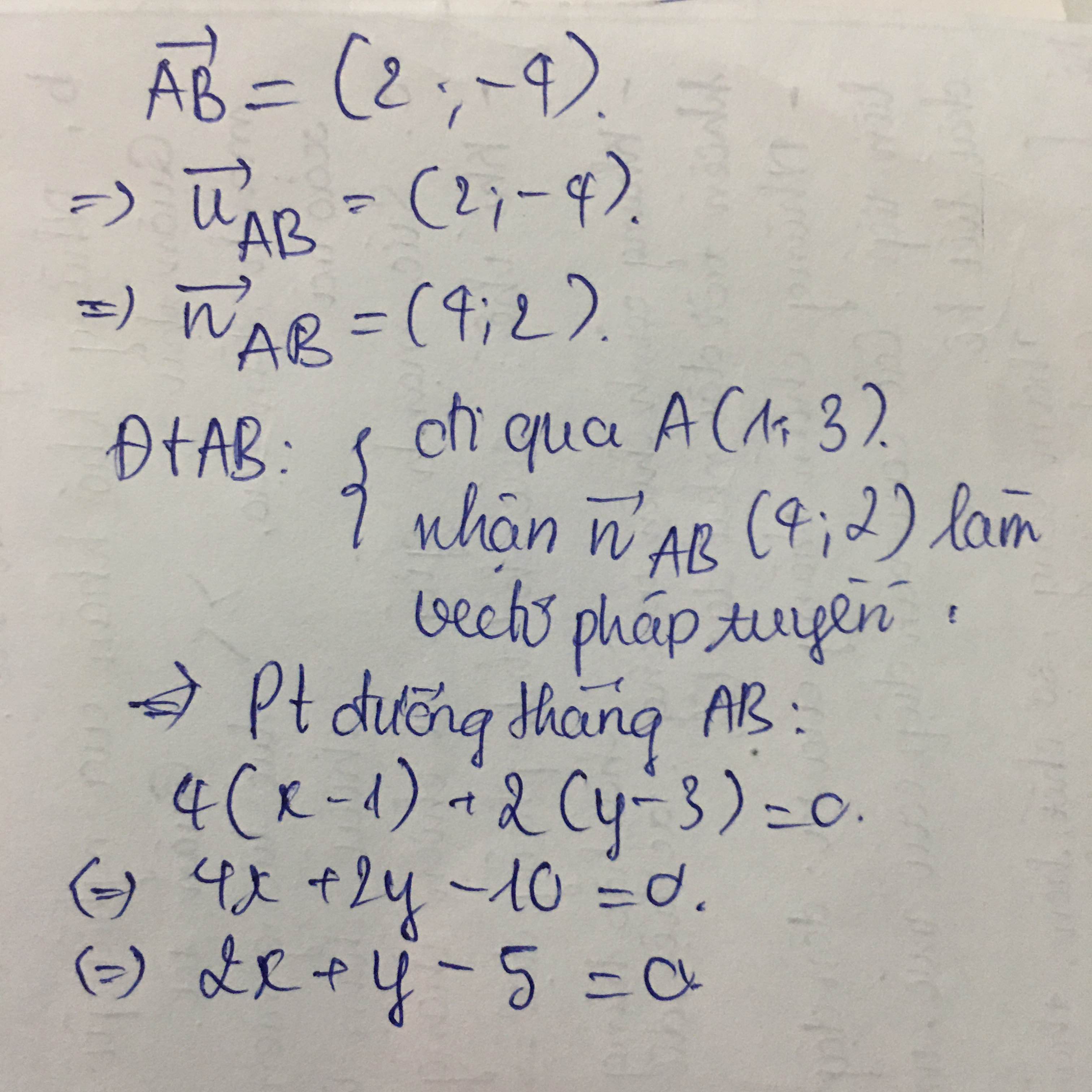
Ta tìm được duong thẳng d1 đi qua A có véc tơ chỉ phương là BC và dường thẳng d2 đi qua A và trung điểm của BC
d1:-4x+y+3=0
D2:x-1=0