Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: 2 tia xx' và yy' cắt nhau tại O
\(\Rightarrow\widehat{xOy}\) và \(\widehat{yOx'}\) là 2 góc kề bù
\(\Rightarrow\widehat{xOy}+\widehat{yOx'}=180^0\)
Mà \(2\widehat{xOy}=3\widehat{yOx'}\Rightarrow\widehat{yOx'}=\dfrac{2}{3}\widehat{xOy}\)
\(\Rightarrow\widehat{xOy}+\dfrac{2}{3}\widehat{xOy}=180^0\)
\(\Rightarrow\dfrac{5}{3}\widehat{xOy}=180^0\)
\(\Rightarrow\widehat{xOy}=108^0\)

a) Các cặp góc kề bù
\(\widehat{xOy}\) và \(\widehat{yOx'}\)
\(\widehat{yOx'}\) và \(\widehat{x'Oy'}\)
\(\widehat{x'Oy'}\) và \(\widehat{xOy'}\)
\(\widehat{xOy'}\) và \(\widehat{xOy}\)
Các cặp góc đối:
\(\widehat{xOy}\) và \(\widehat{x'Oy'}\)
\(\widehat{x'Oy}\) và \(\widehat{y'Ox}\)
b) Do \(\widehat{xOy}\) kề bù với \(\widehat{xOy'}\)
\(\Rightarrow\widehat{xOy}+\widehat{xOy'}=180^o\)
\(\Rightarrow\widehat{xOy'}=180^o-70^o=110^o\)
cho hai đường thẳng xx' và yy' cắt nhau tại O. biết x'Oy+xOy'=120o. Tính các góc xOy;yOx';x'Oy';y'Ox


Số đo các góc tạo thành lần lượt là 120 độ; 120 độ; 60 độ và 60 độ

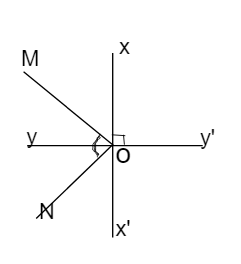
Vì xx' ⊥ yy' tại O (gt)
⇒ ∠x'Oy = 900 (định nghĩa 2 đường thẳng vuông góc)
Ta có: ∠xOy + ∠x'Oy = 1800 (2 góc kề bù)
Thay số: ∠xOy + 900 = 1800
∠xOy = 1800 - 900
∠xOy = 900
Mà OM là tia phân giác của ∠xOy
ON là tia phân giác của ∠yOx'
⇒ ∠mOy = 450
∠yOn = 450
Ta có: ∠mOy + ∠yOn = ∠mOn (2 góc kề nhau)
Thay số: 45+45 = ∠mOn
900 = ∠mOn
∠mOn = 900
Vậy ∠mOn = 900
Ta có hình vẽ:
Ta có: góc xOy + góc xOy' = 1800 (kề bù)
Mà góc xOy = 3.góc xOy'
=> 3.góc xOy' + góc xOy' = 1800
=> 4.góc xOy' = 1800
=> góc xOy' = 1800 / 4 = 45
Ta có: góc xOy = 3.góc xOy'
=> góc xOy = 3.450 = 1350
Ta có: góc xOy = góc x'Oy' = 1350 (đđ)
Ta có: góc xOy' = góc x'Oy = 450 (đđ).
Ta có:
\(\widehat{xOy}+\widehat{xOy'}=180^o\) (1)
mà theo bài ra: \(\widehat{xOy}=3.\widehat{xOy'}\)(2)
Thay (2) vào (1) ta được:
\(3.\widehat{xOy'}+\widehat{xOy'}=180^o\Rightarrow4\widehat{xOy'}=180^o\)
\(\Rightarrow\widehat{xOy'}=45^o\)
\(\Rightarrow\widehat{xOy}=180^o-\widehat{xOy'}=180^o-45^o=135^o\)
Ta lại có:
\(\left\{{}\begin{matrix}\widehat{xOy'}=\widehat{x'Oy}\left(d.d\right)\\\widehat{xOy}=\widehat{x'Oy'}\left(d.d\right)\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\widehat{xOy'}=\widehat{x'Oy}=45^o\\\widehat{xOy}=\widehat{x'Oy'}=135^o\end{matrix}\right.\)
Vậy...........
Chúc bạn học tốt!!!