Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 2:
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=\left(2a\right)^2+\left(2a\sqrt{3}\right)^2=16a^2\)
=>BC=4a
Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{1}{2}\)
nên \(\widehat{ABC}=30^0\)
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}=60^0\)
Lấy điểm E sao cho \(\overrightarrow{AB}=\overrightarrow{BE}\)
=>B là trung điểm của AE
=>\(\widehat{CBE}+\widehat{CBA}=180^0\)(hai góc kề bù)
=>\(\widehat{CBE}=180^0-30^0=150^0\)
\(\overrightarrow{AB}\cdot\overrightarrow{BC}=\overrightarrow{BE}\cdot\overrightarrow{BC}\)
\(=BE\cdot BC\cdot cos\left(\overrightarrow{BE};\overrightarrow{BC}\right)\)
\(=2a\sqrt{3}\cdot4a\cdot cos150=-12a^2\)
\(\left|\overrightarrow{AB}-\overrightarrow{AC}\right|=\left|\overrightarrow{AB}+\overrightarrow{CA}\right|=\left|\overrightarrow{CB}\right|=CB=4a\)

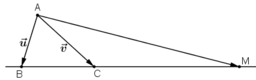
Ta có: 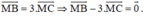
Theo quy tắc ba điểm ta có:
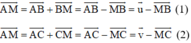
Lấy (1) trừ 3 lần (2) ta được:
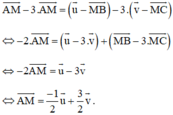

\(a,AC=\sqrt{\left(4-7\right)^2+\left(6-\dfrac{3}{2}\right)^2}=\sqrt{9+\dfrac{81}{4}}=\dfrac{3\sqrt{13}}{2}\\ AB=\sqrt{\left(4-1\right)^2+\left(6-4\right)^2}=\sqrt{9+4}=\sqrt{13}\\ BC=\sqrt{\left(1-7\right)^2+\left(4-\dfrac{3}{2}\right)^2}=\sqrt{36+\dfrac{25}{4}}=\dfrac{13}{2}\)