
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


II/ Bài tập tham khảo:
Bài 4:
\(A=sin^21^0+sin^22^0+sin^23^0+...+sin^288^0+sin^289^0\)
\(A=\left(sin^21^0+sin^289^0\right)+\left(sin^22^0+sin^288^0\right)+...+\left(sin^244^0+sin^246^0\right)+sin^245^0\)
\(A=\left(sin^21^0+cos^21^0\right)+\left(sin^22^0+cos^22^0\right)+...+\left(sin^244^0+cos^244^0\right)+\left(\frac{\sqrt{2}}{2}\right)^2\)
\(A=1+1+...+1+1\)(45 số hạng tất cả)
(vì \(\sin^2\alpha+\cos^2\alpha=1\)và \(\left(\frac{\sqrt{2}}{2}\right)^2=1\)
A = 45

Câu 5:
$\frac{20}{\sqrt{5}}=\frac{20\sqrt{5}}{5}=4\sqrt{5}$
Câu 6:
\(\frac{3}{\sqrt{5}+\sqrt{2}}+\frac{3}{\sqrt{5}-\sqrt{2}}=3.\frac{\sqrt{5}-\sqrt{2}+\sqrt{5}+\sqrt{2}}{(\sqrt{5}+\sqrt{2})(\sqrt{5}-\sqrt{2})}=3.\frac{2\sqrt{5}}{5-2}=2\sqrt{5}\)
Câu 7:
1. ĐKXĐ: $x\neq 1; x\geq 0$
\(A=\left[\frac{\sqrt{x}(\sqrt{x}+1)}{\sqrt{x}+1}+1\right]:\left[\frac{\sqrt{x}(\sqrt{x}-1)}{\sqrt{x}-1}-1\right]=(\sqrt{x}+1):(\sqrt{x}-1)\)
\(=\frac{\sqrt{x}+1}{\sqrt{x}-1}\)
2.
\(A< 1\Leftrightarrow \frac{\sqrt{x}+1}{\sqrt{x}-1}-1<0\Leftrightarrow \frac{2}{\sqrt{x}-1}<0\)
\(\Leftrightarrow \sqrt{x}-1<0\Leftrightarrow x< 1\)
Kết hợp ĐKXĐ suy ra $0\leq x< 1$

a) 45 . 80
= 5 . 9 . 5 . 16 = 5 2 . 3 2 . 4 2 = 5 . 3 . 4 = 60

Câu 1:
a: \(\sqrt{9\cdot25}=3\cdot5=15\)
b: \(=3\sqrt{2}\cdot\sqrt{2}+4\sqrt{2}\cdot\sqrt{2}-5\sqrt{2}\cdot\sqrt{2}\)
=6+8-10
=4

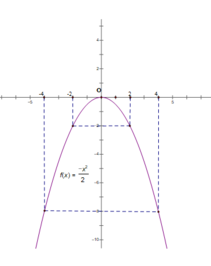
a) Vẽ đồ thị hàm số (P): y = (-1)/2 x 2
Bảng giá trị :
| x | -4 | -2 | 0 | 2 | 4 |
| y = (-1)/2 x2 | -8 | -2 | 0 | -2 | -8 |
Đồ thị hàm số y = (-1)/2 x 2 là một đường Parabol nằm phía dưới trục hoành, nhận trục tung làm trục đối xứng, nhận gôc tọa độ O(0;0) làm đỉnh và là điểm cao nhất.





Câu 1:
\(a,B=\left[\sqrt{a}-\dfrac{\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{\sqrt{a}+1}\right]\left[\sqrt{a}+\dfrac{\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}{\sqrt{a}-1}\right]\\ B=\left(-a+2\sqrt{a}-1\right)\left(a+2\sqrt{a}+1\right)\\ B=-\left(\sqrt{a}-1\right)^2\left(\sqrt{a}+1\right)^2=-\left(a-1\right)^2\\ b,B=25\Leftrightarrow-\left(a-1\right)^2=25\left(\text{vô lí}\right)\\ \Leftrightarrow a\in\varnothing\)