Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABI vuông tại I và ΔACI vuông tại I có
AI chung
BI=CI
Do đó: ΔABI=ΔACI
b: Ta có: ΔABI=ΔACI
nên AB=AC
hay ΔABC cân tại A
c: Xét tứ giác ABDC có
I là trung điểm của BC
I là trung điểm của AD
Do đó:ABDC là hình bình hành
Suy ra: AB//CD

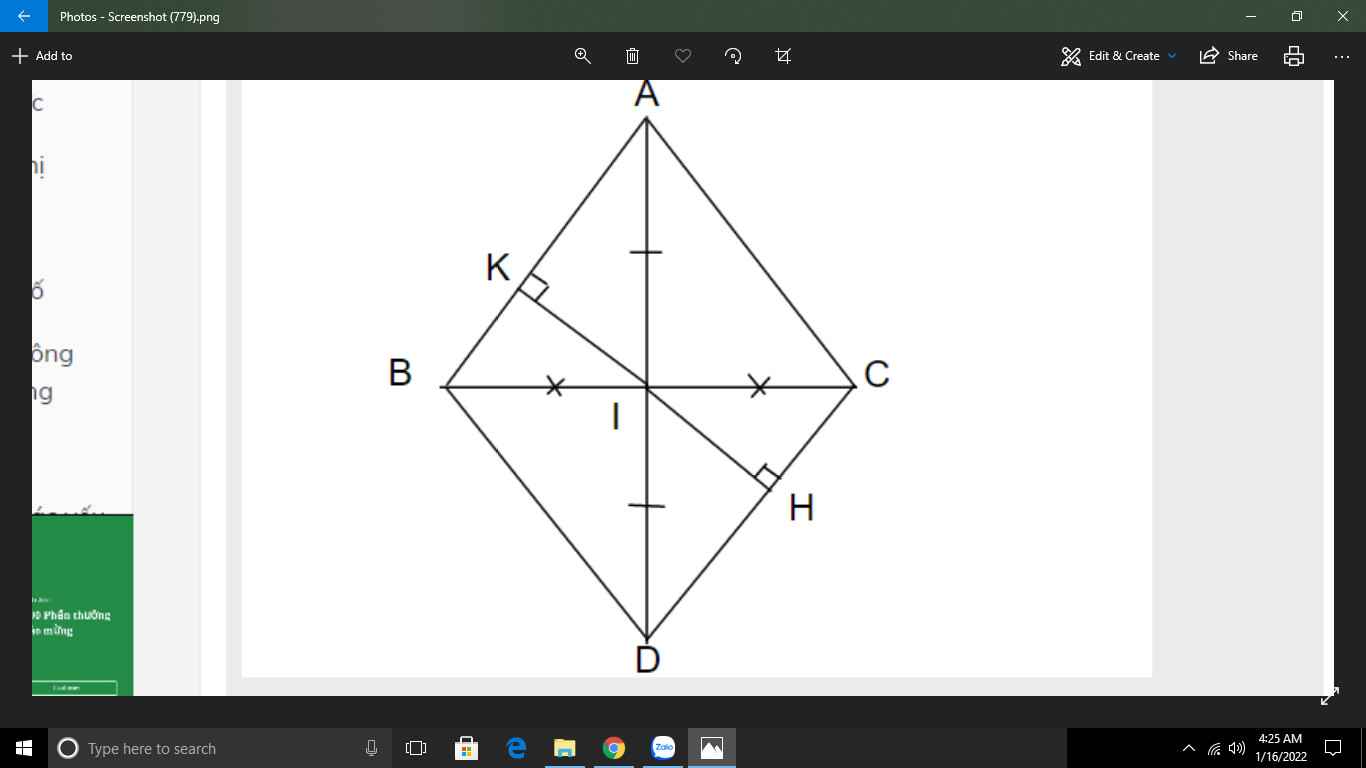
\(\text{a)}\text{Xét }\Delta ABI\text{ và }\Delta ACI\text{ có:}\)
\(AB=AC\left(gt\right)\)
\(BI=CI\text{(I trung điểm BC)}\)
\(AI\text{ chung}\)
\(\Rightarrow\Delta ABI=\Delta ACI\left(c.c.c\right)\)
\(\text{b)Xét }\Delta AIC\text{ và }\Delta DIB\text{ có:}\)
\(AI=DI\left(gt\right)\)
\(\widehat{AIC}=\widehat{DIB}\text{(đối đỉnh)}\)
\(IC=IB\)
\(\Rightarrow\Delta AIC=\Delta DIB\left(c.g.c\right)\)
\(\Rightarrow\widehat{DIB}=\widehat{ICA}\text{(2 góc tương ứng)}\)
\(\text{mà chúng so le trong}\)
\(\Rightarrow AC=BD\)
\(\text{c)Xét }\Delta IKB\text{ và }\Delta IHC\text{ có:}\)
\(\widehat{IKB}=\widehat{IHC}=90^0\)
\(IB=IC\)
\(\widehat{KIB}=\widehat{CIH}\text{(đối đỉnh)}\)
\(\Rightarrow\Delta IKB=\Delta IHC\left(ch-gn\right)\)
\(\Rightarrow IK=IH\)
\(\text{Hình có chỗ nào bạn ko thấy rõ thì ib riêng cho mik nghe:3}\)

xét tam giác ABE và tam giác ADE
AE chung
góc BAE = góc DAE(AE la tia phân giác của góc E)
AB = AD ( gt)
=> tam giác ABE = tam giac DAE ( c.g.c)
b) xét tam giác ABI và tam giác ADI
AI chung
góc BAE = góc DAE
tam giác ABI=tam giác ADI
=> BI = DI ( 2 cạnh t/ứ )
=> I là trung điểm của BD

Ta có : Tam giác ABM cân tại B
=>MAB^=AMB^ (1)
Lại có : IMB^=IAB^=90* (2)
Từ 1 và 2 : +)IAM^=90*-MAB^
+)IMA^ =90*-AMB^
=>IAM^=IMA^
=>Tam giác IAM cân tại I
=>IA=iM
''∠'' là góc nhé.
a) Vì ∆ABC vuông tại A (GT)
=> ∠BAC = 90o (ĐN) (1)
Vì IM ⊥ BC (GT)
=> ∠IMB = 90o
Mà ∠BAC = 90o (Theo (1))
(Ngoặc ''}'' 2 điều trên)
=> ∠BAC = ∠IMB = 90o
Hay ∠BAI = ∠IMB = 90o (2)
Xét ∆ABI và ∆MBI có :
∠BAI = ∠IMB = 90o (Theo (2))
BI chung
BA = BM (Gt)
=> ∆ABI = ∆MBI (cạnh huyền - cạnh góc vuông)
=> AI = IM (2 cạnh tương ứng) (3)
b) Ta có : ∠BAC + ∠NAC = 180o (2 góc kề bù)
Mà ∠BAC = 90o (Theo (1))
=> 90o + ∠NAC = 180o
=> ∠NAC = 180o - 90o = 90o
Vì IM ⊥ BC (GT) => ∠IMC = 90o (ĐN)
(Ngoặc ''}'' 2 điều trên)
=> ∠NAC = ∠IMC = 90o
Hay ∠NAI = ∠IMC = 90o (4)
Lại có : ∠I1 = ∠I2 (2 góc đối đỉnh) (5)
Xét ∆ANI và ∆MCI có :
∠NAI = ∠IMC = 90o (Theo (4))
AI = MI (Theo (3))
∠I1 = ∠I2 (Theo (5))
=> ∆ANI = ∆MCI (g.c.g)
=> AN = MC (2 cạnh tương ứng)
Mà AN + BA = BN
MC + BM = BC
BA = BM (GT)
(Ngoặc ''}'' 4 điều trên)
=> BN = BC
=> ∆NBC cân tại B (ĐN)
P/s : Xin lỗi, mình chỉ làm được đến đây thôi, nghỉ nhiều quá nên mình ngu hẳn, có gì mình nghiên cứu lại sau :(.

a: Xét ΔAIB và ΔAIC có
AB=AC
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC
b: Ta có: ΔABC cân tại A
mà AI là đường trung tuyến
nên AI là đường cao
c: Xét tứ giác ABEC có
I là trung điểm của AE
I là trung điểm của BC
Do đó: ABEC là hình bình hành
Suy ra: AB//EC

a: Xét ΔIAB và ΔIEC có
IA=IE
\(\widehat{AIB}=\widehat{EIC}\)
IB=IC
Do đó: ΔIAB=ΔIEC
b: Xét tứ giác ACEB có
M là trung điểm của AE
M là trung điểm của BC
Do đó: ACEB là hình bình hành
Suy ra;AB//EC
c: Ta có: AB//EC
mà AB⊥AC
nên EC⊥AC
hay \(\widehat{ACE}=90^0\)

a/ Xét △ABM và △DMC có:
\(\begin{matrix}AM=MD\left(gt\right)\\MB=MC\left(gt\right)\\\hat{AMB}=\hat{CMD}\left(đối\text{ }đỉnh\right)\end{matrix}\)
\(\Rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\) (đpcm).
b/ Ta có: \(\Delta AMB=\Delta DMC\left(cmt\right)\)
\(\Rightarrow\hat{MAB}=\hat{MDC}\); hai góc ở vị trí so le trong.
Vậy: AB // CD (đpcm).
c/ Xét △BAE có:
\(\begin{matrix}BH\perp AE\left(gt\right)\\AH=HE\left(gt\right)\end{matrix}\)
⇒ BH vừa là đường cao, vừa là đường trung tuyến.
⇒ △BAE cân tại B.
\(\Rightarrow BE=BA\). Mà \(AB=CD\left(\Delta AMB=\Delta DMC\right)\)
Vậy: BE = CD (đpcm).
b: Xét tứ giác ABDC có
I là trung điểm của BC
I là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB=CD