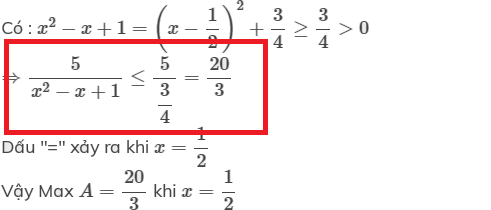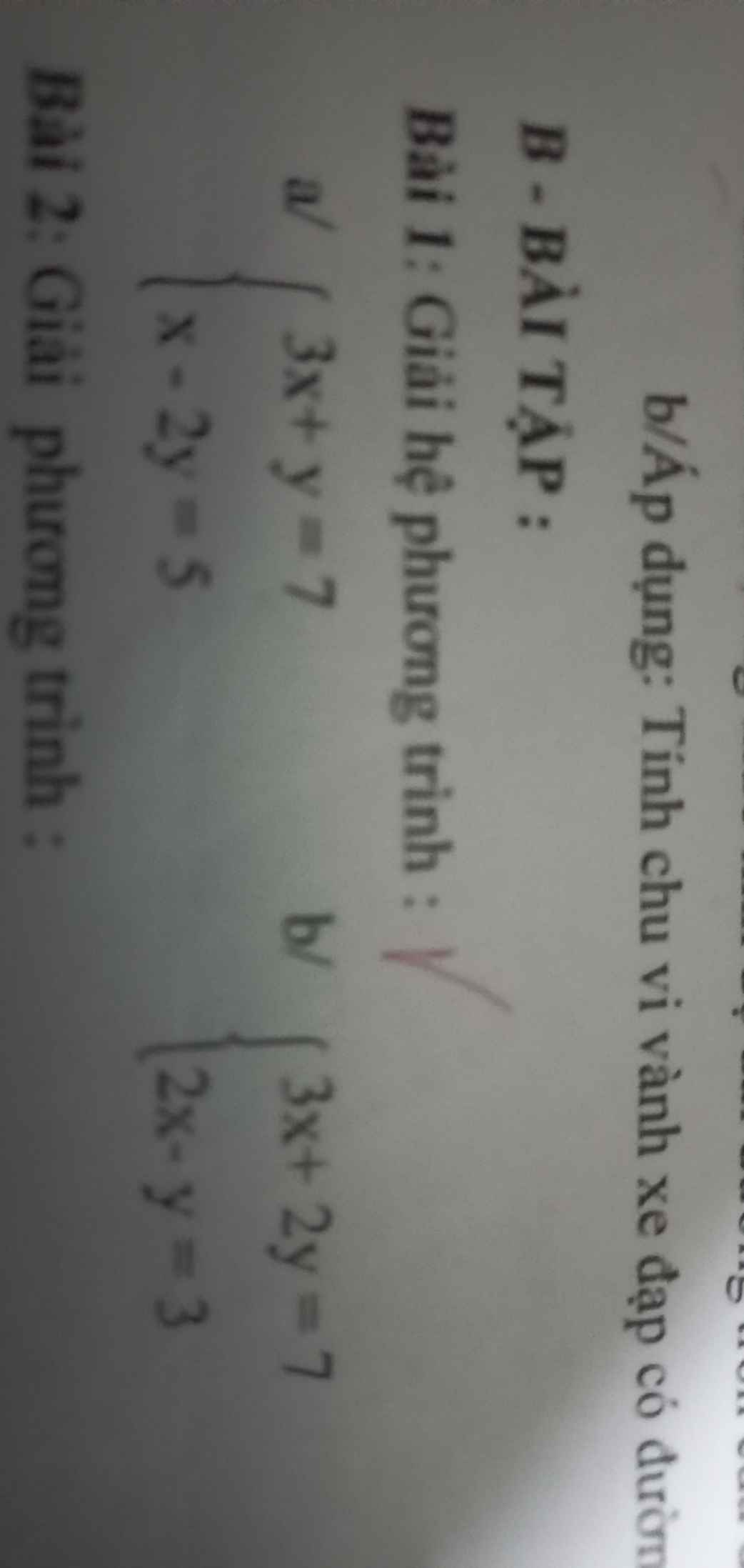K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 8 2018
chưa ai lm thì mèo lm nha, chọn bài dễ nhất
Bài 1:
a,\(\sqrt{4+2\sqrt{3}}-\sqrt{4-2\sqrt{3}}\)
\(=\sqrt{3+2.\sqrt{3}.1+1}-\sqrt{3-2.\sqrt{3}.1+1}\)
\(=\sqrt{\left(\sqrt{3}+1\right)^2}-\sqrt{\left(\sqrt{3}-1\right)^2}\)
\(=\sqrt{3}+1-\left(\sqrt{3}-1\right)=\sqrt{3}+1-\sqrt{3}+1=2\)
b,\(\sqrt{94+42\sqrt{5}}-\sqrt{94-42\sqrt{5}}\)
\(=\sqrt{49+2.7.3\sqrt{5}+45}-\sqrt{49-2.7.3\sqrt{5}+45}\)
\(=\sqrt{\left(7+3\sqrt{5}\right)^2}-\sqrt{\left(7-3\sqrt{5}\right)^2}\)
\(=7+3\sqrt{5}-\left(7-3\sqrt{5}\right)=6\sqrt{5}\)
9 tháng 8 2018
Bài 2: (chả biết bạn bấm máy hay làm cách nào, nhưng nếu tính tay thì mk hay làm cách này)
a,\(\sqrt{\dfrac{0,144}{10}}=\sqrt{\dfrac{144}{10000}}=\dfrac{\sqrt{144}}{\sqrt{10000}}=\dfrac{12}{100}=\dfrac{3}{25}\)
b,\(\sqrt{\dfrac{1890}{1000}}=\sqrt{\dfrac{189}{100}}=\dfrac{\sqrt{189}}{\sqrt{100}}=\dfrac{\sqrt{9.21}}{10}=\dfrac{3\sqrt{21}}{10}\)
c,\(\dfrac{\sqrt{0,225}}{\sqrt{10}}=\dfrac{\sqrt{225}}{\sqrt{10000}}=\dfrac{15}{100}=\dfrac{3}{20}\)
d,\(\dfrac{\sqrt{8a^5b}}{\sqrt{2ab}}=\sqrt{4a^4b}=2a^2\sqrt{b}\) với a,b > 0
LP
0
NH
8
13 tháng 7 2018
Bài 16: Biểu thức sau đây xác định với giá trị nào của x?
a) \(\sqrt{\left(x-1\right)\left(x-3\right)}\) c) \(\sqrt{\frac{x-2}{x+3}}\)
b) \(\sqrt{x^2-4}\) d) \(\sqrt{\frac{2+x}{5-x}}\)
Bài 22: Với n là số tự nhiên, chứng minh đẳng thức:
\(\sqrt{\left(n+1\right)^2}+\sqrt{n^2}=\left(n+1\right)^2-n^2\)
28 tháng 6 2021
Bởi vì ta có tính chất:
`a>=b>0=>1/a<=1/b`
GTLN bởi vì có dấu `<=`
LA
3 tháng 5 2022
a)
\(\left\{{}\begin{matrix}3x+y=7\left(1\right)\\x-2y=5\left(2\right)\end{matrix}\right.\)
lấy (1) . 2 + (2)
<=> 7x = 19 => x = \(\dfrac{19}{7}\)
thay x = \(\dfrac{19}{7}\) vào phương trình (2) ta có
\(\dfrac{19}{7}\) - 2y = 5
<=> 2y = \(\dfrac{-16}{7}\) => y = \(\dfrac{-8}{7}\)
vậy (x;y) = { ( \(\dfrac{19}{7}\);\(\dfrac{-8}{7}\) ) }
b)
\(\left\{{}\begin{matrix}3x+2y=7\left(1\right)\\2x-y=3\left(2\right)\end{matrix}\right.\)
lấy (2).2 + (1)
=> 7x = 13 => x = \(\dfrac{13}{7}\)
thay x = \(\dfrac{13}{7}\) vào phương trình 2 ta có
\(\dfrac{13}{7}\) - 2y = 5
<=> 2y = \(\dfrac{-22}{7}\) => y = \(\dfrac{-11}{7}\)
vậy (x;y) = {(\(\dfrac{13}{7}\);\(\dfrac{-11}{7}\))}
30 tháng 8 2023
Tập hợp A là các số chính phương có 2 chữ số
\(A=\left\{16;25;36;49;64;81\right\}\)
Tập hợp B là các số chia 4 dư 1 :
\(B=\left\{25;49;81\right\}\)