Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔHEB vuông tại E và ΔHDC vuông tại D có
góc EHB=góc DHC
=>ΔHEB đồng dạng với ΔHDC
b: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AB*AE; AD/AB=AE/AC
c: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc A chung
=>ΔADE đồng dạng với ΔABC
=>góc AED=góc ACB

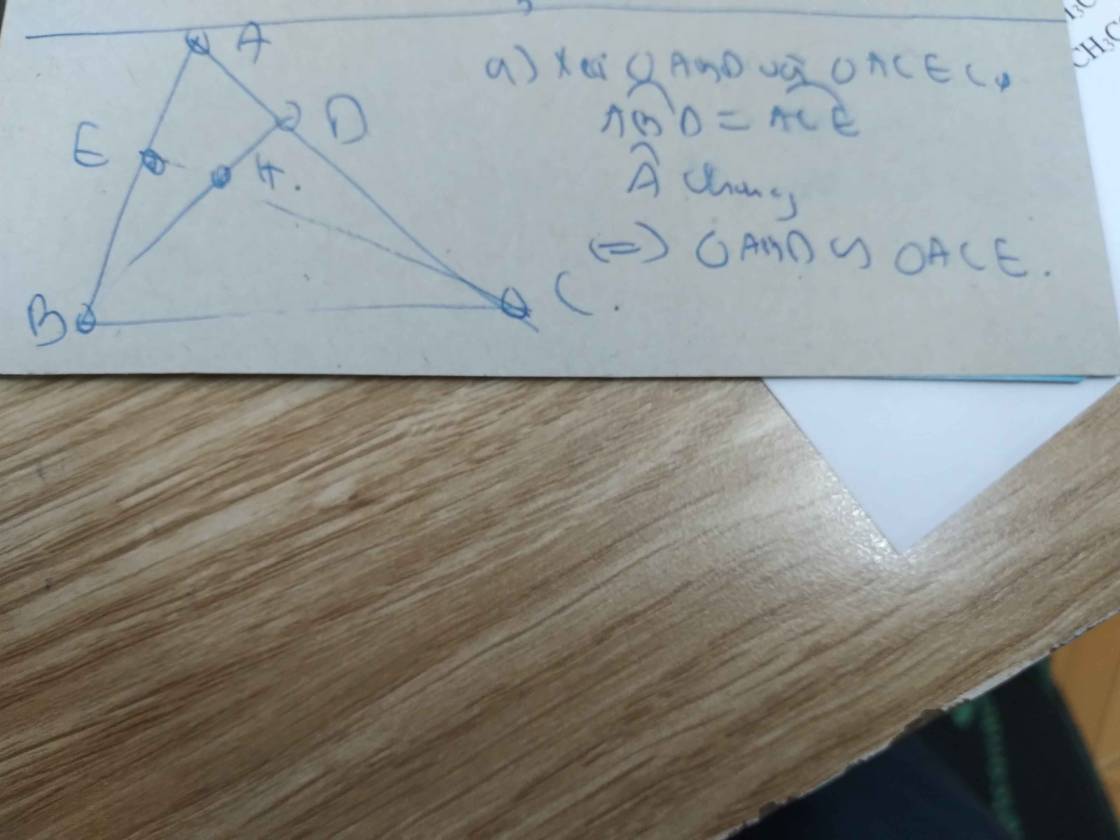
a) Xét \(\Delta ABD\)và \(\Delta ACE\)có:
\(\widehat{ADB}=\widehat{AEC}=90^0\)
\(\widehat{BAC}\) chung
suy ra: \(\Delta ABD~\Delta ACE\) (g.g)
\(\Rightarrow\)\(\frac{AB}{AC}=\frac{AD}{AE}\)
\(\Rightarrow\)\(AB.AE=AC.AD\)
b) \(\frac{AB}{AC}=\frac{AD}{AE}\) (câu a)
\(\Rightarrow\)\(\frac{AE}{AC}=\frac{AD}{AB}\)
Xét \(\Delta AED\)và \(\Delta ACB\)có:
\(\frac{AE}{AC}=\frac{AD}{AB}\) (cmt)
\(\widehat{EAD}\) chung
suy ra: \(\Delta AED~\Delta ACB\) (g.g)
c) Kẻ \(HK\perp BC\) \(\left(K\in BC\right)\)
C/m: \(\Delta BKH~\Delta BDC\)(g.g) \(\Rightarrow\) \(\frac{BK}{BD}=\frac{BH}{BC}\)\(\Rightarrow\)\(BH.BD=BK.BC\) (1)
\(\Delta CKH~\Delta CEB\)(g.g) \(\Rightarrow\)\(\frac{CK}{CE}=\frac{CH}{CB}\)\(\Rightarrow\)\(CE.CH=CK.BC\) (2)
Lấy (1) + (2) theo vế ta được: \(BH.BD+CE.CH=BK.BC+CK.BC=BC^2\) (đpcm)

a, Xét tam giác ADB và tam giác AEC có
^ADB = ^AEC = 900
^DAB _ chung
Vậy tam giác ADB ~ tam giác AEC (g.g)
b, \(\dfrac{AD}{AE}=\dfrac{AB}{AC}\Rightarrow AD.AC=AB.AE\)
c, \(\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{DE}{BC}\right)^2=\dfrac{1}{4}\)

a) Chứng minh tam giác AED đông dang tam giác ACB
b) Kẻ HI vuông góc BC
Có BHxBD+CHxCE=BC^2 bằng xét 2 cặp tam giác đông dạng.

a: Xet ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạng vơi ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AE*AB; AD/AB=AE/AC
b: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc DAE chung
=>ΔADE đồng dạng với ΔABC
c: \(DB=\sqrt{5^2-3^2}=4\left(cm\right)\)
\(S_{BAC}=\dfrac{1}{2}\cdot4\cdot6=12\left(cm^2\right)\)

a) Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{DAB}\) chung
Do đó: ΔADB\(\sim\)ΔAEC(g-g)