Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔAEC vuông tại E và ΔAHB vuông tại H có
\(\widehat{BAH}\) chung
Do đó: ΔAEC\(\sim\)ΔAHB(g-g)
Suy ra: \(\dfrac{AE}{AH}=\dfrac{AC}{AB}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AE\cdot AB=AH\cdot AC\)(đpcm)
b) Ta có: \(\dfrac{AE}{AH}=\dfrac{AC}{AB}\)(cmt)
nên \(\dfrac{AE}{AC}=\dfrac{AH}{AB}\)
Xét ΔAEH và ΔACB có
\(\dfrac{AE}{AC}=\dfrac{AH}{AB}\)(cmt)
\(\widehat{EAH}\) chung
Do đó: ΔAEH\(\sim\)ΔACB(c-g-c)
Suy ra: \(\widehat{AEH}=\widehat{ACB}\)(hai góc tương ứng)

a: Xét ΔHEB vuông tại E và ΔHDC vuông tại D có
góc EHB=góc DHC
=>ΔHEB đồng dạng với ΔHDC
b: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AB*AE; AD/AB=AE/AC
c: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc A chung
=>ΔADE đồng dạng với ΔABC
=>góc AED=góc ACB

B1): a): +)Ta có csc đường cao BD, CE cắt nhau tại I => BD vg góc vs AC; CE vg góc vs AB
+)Xét tg AEC và tg ADB, có: AEC=AHB=90( BD vg góc vs AC; CE vg góc vs AB )
BAC chung
Do đó: tg AEC ~ tg ADB ( gg)
=> AE/AD= AC/AB=> AE*AB=AD*AC (đpcm)
b) : Gợi ý hoi :)): Kẻ đcao AF xuống BC, sẽ đi qua điểm I; c/m ED//BC=> c/m đc tg AED~tg ABC theo trường hợp cgc, từ đó ta sẽ có đc 2 góc AED = ABC ( vì 2 tg trên ~ vs nhau )
a, Vì BM là phân giác ^B nên : \(\frac{AB}{BC}=\frac{AM}{MC}\)( t/c )
\(\Rightarrow\frac{MC}{BC}=\frac{AM}{AB}\)( tỉ lệ thức )
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{MC}{BC}=\frac{AM}{AB}=\frac{MC+AM}{BC+AB}=\frac{5}{11}\)
\(\Rightarrow\frac{MC}{6}=\frac{5}{11}\Rightarrow MC=\frac{30}{11}\)cm
\(\Rightarrow\frac{AM}{5}=\frac{5}{11}\Rightarrow AM=\frac{25}{11}\)cm

a) Chứng minh tam giác AED đông dang tam giác ACB
b) Kẻ HI vuông góc BC
Có BHxBD+CHxCE=BC^2 bằng xét 2 cặp tam giác đông dạng.
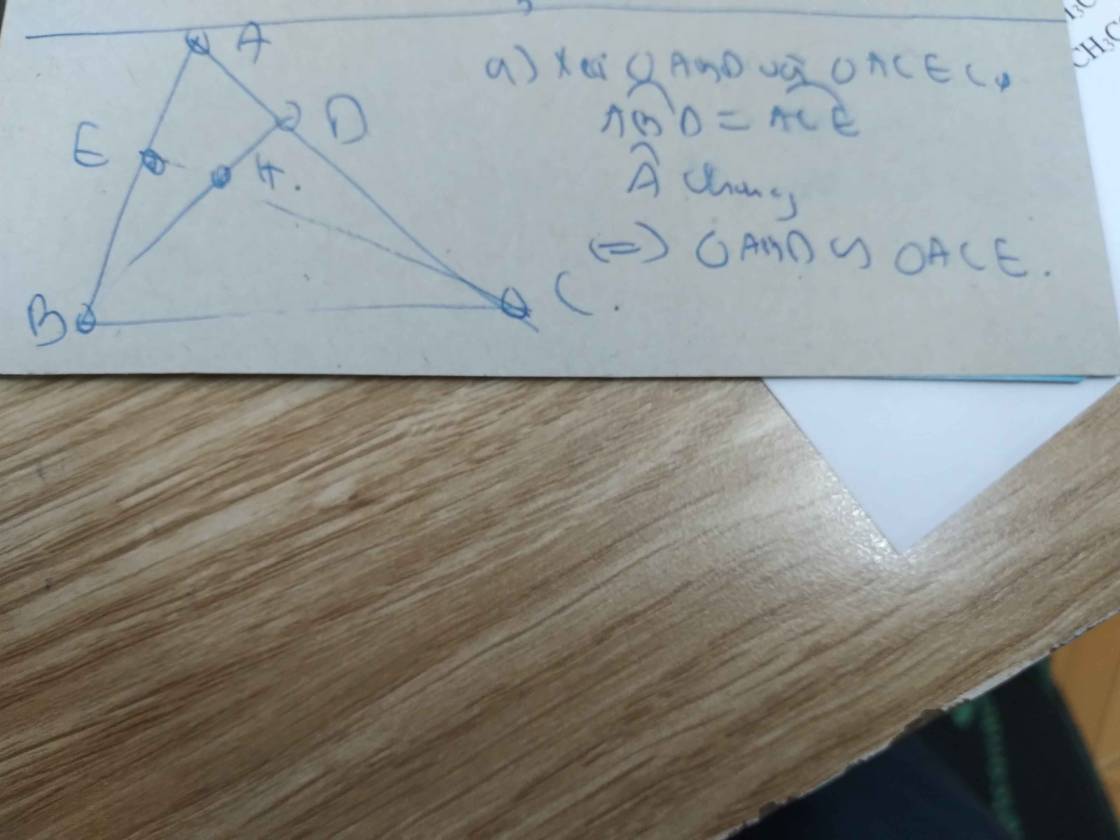

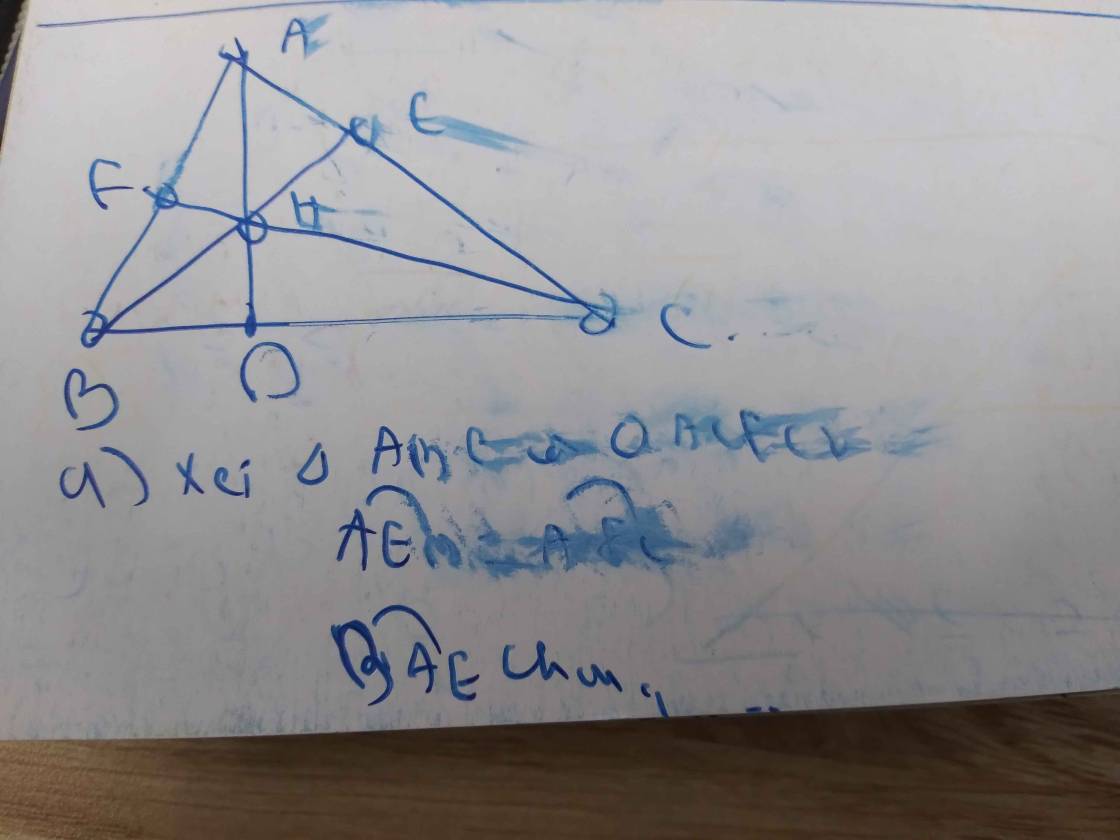

a: Xet ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạng vơi ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AE*AB; AD/AB=AE/AC
b: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc DAE chung
=>ΔADE đồng dạng với ΔABC
c: \(DB=\sqrt{5^2-3^2}=4\left(cm\right)\)
\(S_{BAC}=\dfrac{1}{2}\cdot4\cdot6=12\left(cm^2\right)\)