K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 10 2021
\(1,\\ x+2\ge0\Leftrightarrow x\ge-2\)
\(\Leftrightarrow A=\)\([-2;+\infty)\)
\(5-x\ge0\Leftrightarrow x\le5\)
\(\Leftrightarrow B=\)\((-\infty;5]\)
\(\Leftrightarrow A\cap B=\left[-2;5\right]\)
\(2,A\cup B=\varnothing\)
AH
Akai Haruma
Giáo viên
1 tháng 12 2021
Lời giải:
$\overrightarrow{MA}=(1-x, 3-y), \overrightarrow{MB}=(4-x, 2-y)$
Để $MAB$ là tam giác vuông cân tại $M$ thì:
\(\left\{\begin{matrix}
\overrightarrow{MA}.\overrightarrow{MB}=0\\
MA^2=MB^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
(1-x)(4-x)+(3-y)(2-y)=0\\
(1-x)^2+(3-y)^2=(4-x)^2+(2-y)^2\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x^2-5x+y^2-5y+10=0\\ 6x-2y-10=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x^2-5x+y^2-5y+10=0\\ y=3x-5\end{matrix}\right.\)
\(\Leftrightarrow (x,y)=(2,1), (3,4)\)
TM
7 tháng 9 2023
\(P\cap Q=\varnothing\Leftrightarrow\left[{}\begin{matrix}a+1< -5\\a-1>4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a< -6\\a>5\end{matrix}\right.\)
\(\Rightarrow P\cap Q\ne\varnothing\Leftrightarrow-6\le a\le5\)
Vậy: \(a\in\left[-6;5\right]\).
8 tháng 9 2023
Bài 18 :
\(\left(-\infty;9a\right)\cap\left(\dfrac{4}{a};+\infty\right)\ne\varnothing\) \(\left(a< 0\right)\)
\(\Rightarrow9a>\dfrac{4}{a}\)
\(\Leftrightarrow9a-\dfrac{4}{a}>0\)
\(\Leftrightarrow\dfrac{9a^2-4}{a}>0\)
\(\Leftrightarrow9a^2-4< 0\left(a< 0\right)\)
\(\Leftrightarrow9a^2< 4\)
\(\Leftrightarrow a^2< \dfrac{4}{9}=\left(\dfrac{2}{3}\right)^2\)
\(\Leftrightarrow-\dfrac{2}{3}< a< \dfrac{2}{3}\)
mà \(a< 0\)
\(\Leftrightarrow-\dfrac{2}{3}< a< 0\)
AH
Akai Haruma
Giáo viên
1 tháng 12 2021
Tham khảo tại link sau:
https://hoc24.vn/cau-hoi/ai-giup-em-cau-2-voi-a.3401576227354
15 tháng 10 2021
Bài 6:
ĐK: \(9a< \dfrac{4}{a}\Leftrightarrow a^2< \dfrac{4}{9}\Leftrightarrow-\dfrac{2}{3}< a< \dfrac{2}{3}\)
15 tháng 10 2021
Bài 7:
ĐK: \(a=\dfrac{4}{a}\Leftrightarrow a^2=4\Leftrightarrow\left[{}\begin{matrix}a=2\\a=-2\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 8 2021
3.
\(0\le sin^22x\le1\Rightarrow\dfrac{1+4.0}{5}\le y\le\dfrac{1+4.1}{5}\)
\(\Rightarrow\dfrac{1}{5}\le y\le1\)
\(y_{min}=\dfrac{1}{5}\) khi \(sin2x=0\Rightarrow x=\dfrac{k\pi}{2}\)
\(y_{max}=1\) khi \(cos2x=0\Rightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
4.
\(y=2sin^2x-\left(1-2sin^2x\right)=4sin^2x-1\)
Do \(0\le sin^2x\le1\Rightarrow-1\le y\le3\)
\(y_{min}=-1\) khi \(sinx=0\Rightarrow x=k\pi\)
\(y_{max}=3\) khi \(cosx=0\Rightarrow x=\dfrac{\pi}{2}+k\pi\)
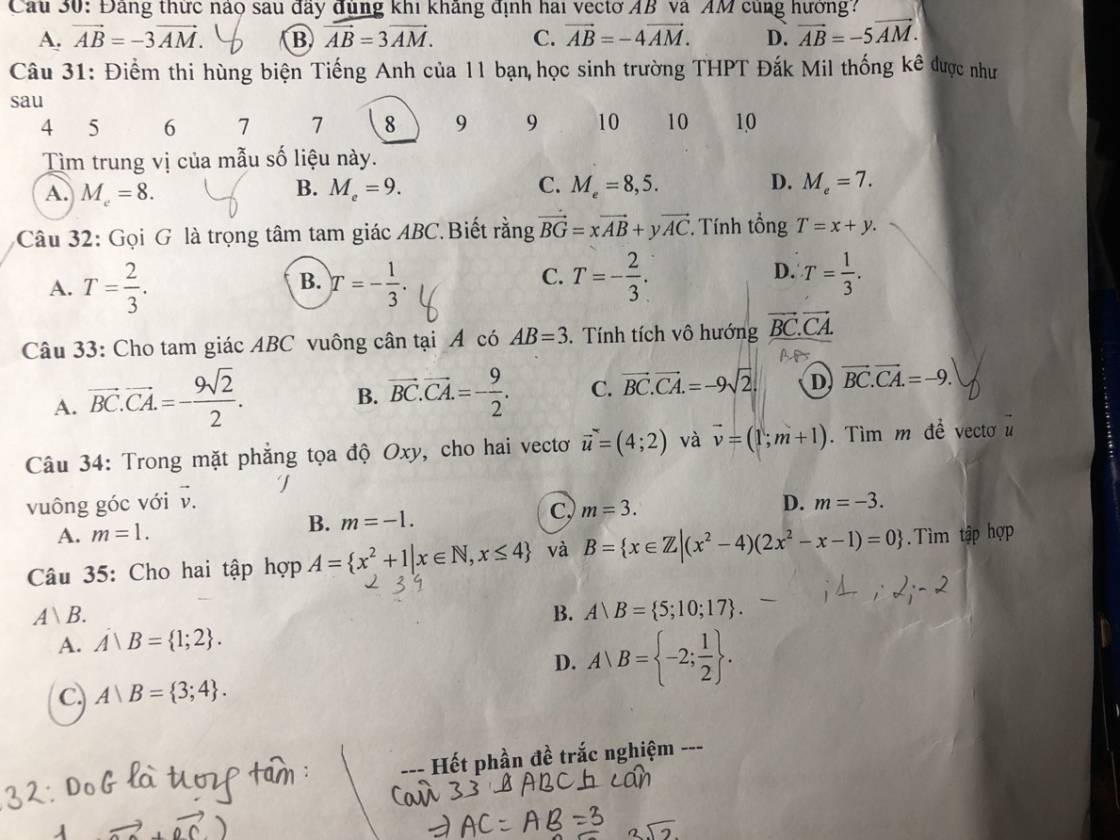
Câu 33:
Vì ΔABC vuông cân tại A nên \(\widehat{B}=\widehat{C}=45^0\)
ΔABC vuông cân tại A
=>\(BC=AB\cdot\sqrt{2}=3\sqrt{2}\)
\(\overrightarrow{BC}\cdot\overrightarrow{CA}=-\overrightarrow{CB}\cdot\overrightarrow{CA}\)
\(=-CB\cdot CA\cdot cos\left(\overrightarrow{CB};\overrightarrow{CA}\right)\)
\(=-3\cdot3\sqrt{2}\cdot cos45\)
\(=-9\sqrt{2}\cdot\dfrac{\sqrt{2}}{2}=-9\)
=>Chọn D