Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì AB+AC=17 và AB - AC=7.Do đó:
Cạnh AB là:
(17+7):2=12(cm)
Cạnh AC là:
17-12=5(cm)
Xét tam giác ABC vuông tại A
Áp dụng định lý Pi-Ta-Go ta có:
AB2+AC2=BC2
122+52=BC2
BC2=169
BC=13
Vậy cạnh BC=13 cm
giùm để tròn 100 điểm giúp mình nhé các bạn
ủng hộ mình đầu năm cho may nhé
CHÚC MỪNG NĂM MỚI

Theo giả thiết : BC - AC = 3 => AC = BC -3
THeo định lý Pytago : BC2 = AB2 + (BC-3)2
BC2 = AB2 + BC2 - 6BC + 9
0 = AB2 - 6BC + 9 => 6BC = AB2 + 9
6BC = 92 + 9 = 90 => BC = 15 (cm)
Ta có : AC = 15 - 3 = 12 (cm)

`@` `\text {dnammv}`
`a,`
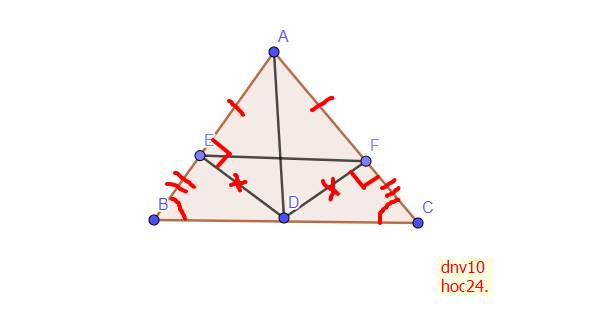
Xét \(\Delta BED\) và \(\Delta CFD\) có:
\(\left\{{}\begin{matrix}\text{BD = CD (D là trung điểm của BC}\\\widehat{\text{B}}=\widehat{\text{C}}\left(\text{ }\Delta\text{ABC cân tại A}\right)\\\widehat{BED}=\widehat{CFD}\left(=90^0\right)\end{matrix}\right.\)
`=> \Delta BED = \Delta CFD (ch-gn)`
`-> \text {BE = CF (2 cạnh tương ứng)}`
`b,`
Vì `\Delta BED = \Delta CFD (a)`
`-> \text {DE = DF (2 cạnh tương ứng)}`
`\text {Xét}` `\Delta DEF:`
`\text {DE = DF}`
`-> \Delta DEF` là `\Delta` cân
`c,`
Vì \(\left\{{}\begin{matrix}\text{AB = AC (tam giác ABC cân tại A)}\\\text{BE = CF (a)}\end{matrix}\right.\)
`-> \text {AE = AF}`
\(\text{Xét }\Delta\text{ AEF}: \)
`\text {AE = AF}`
`-> \Delta AEF` là `\Delta` cân (tại A).
`->`\(\widehat {AEF}= \widehat {AFE}\)\(=\dfrac{180-\widehat{A}}{2}\text{ }\left(1\right)\)
`\Delta ABC` cân tại `A`
`->`\(\widehat {ABC}= \widehat {ACB}=\)\(\dfrac{180-\widehat{A}}{2}\text{ }\left(2\right)\)
Từ `(1)` và `(2)`
`->`\(\widehat {AEF}= \widehat {ABC}\)
Mà `2` góc này nằm ở vị trí đồng vị
`-> \text {EF // BC (tính chất 2 đường thẳng //).}`

1. Vì AB=AH(gt)
AH=AI(gt)
=> AB+AI( áp dụng tính chất bắc cầu
2. Dễ thấy góc BAH=góc BCA vì cả hai góc cùng phụ với góc ABC:
góc BAH+gócHBA=90 độ (tam giác ABH vuông tại H)
góc BCA = góc ABC = 90 độ ( tam giác ABC vuông tại A)
đặt ab/3=ac/4=bc/5=k
=> ab=3k;ac=4k;bc=5k
ta có ab^2 +ac^2=(3k)^2+(4k)^2=9k^2 + 16k^2=25k^5
mà bc^2 = (5k)^2=25k^2
=>tam giác abc là tam giác Vuông