Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) * Vì ABCD là hình bình hành(gt)
=> \(\widehat{A}=\widehat{C}\); \(\widehat{B}=\widehat{D};AD=BC;AB//CD\)( tính chất)
_ Ta có AM là tia phân giác của GÓC A => \(\widehat{A_1}=\widehat{A_2}=\frac{\widehat{A}}{2}\left(1\right)\)
_Ta có CN là tia phân giác của GÓC C =>\(\widehat{C_1}=\widehat{C_2}=\frac{\widehat{C}}{2}\left(2\right)\)
_ Từ (1) (2) => \(\widehat{A_1}=\widehat{C_2}\)
* Xét \(\Delta ADM\) và \(\Delta CBN\)có:
\(\widehat{A_1}=\widehat{C_2}\)( cmt)
AD=BC( cmt)
GÓC B=GÓC D
=> \(\Delta ADM=\Delta CBN\left(g.c.g\right)\)
=>AM=CN (3) ( 2 cạnh tuiwng ứng)
\(\widehat{M_1}=\widehat{N_1}\) ( 2 góc tương ứng)
* Mà AB//CD( gt)
\(N\in AB;M\in CD\left(gt\right)\)
=>BN//CM => \(\widehat{N_1}=\widehat{C_1}\)( 2 góc SLT)
=> \(\widehat{M_1}=\widehat{C_1}\)
Mà 2 góc này ở vị trí Đồng vị
=> AM//CN(4)
* Từ (3)(4)
=> AMCN là hình bình hành
_ Cậu tự vẽ hình xong đặt chỉ số ạ_
_tham khảo bài àm trên đây ạ, chúc cậu học tốt '.'

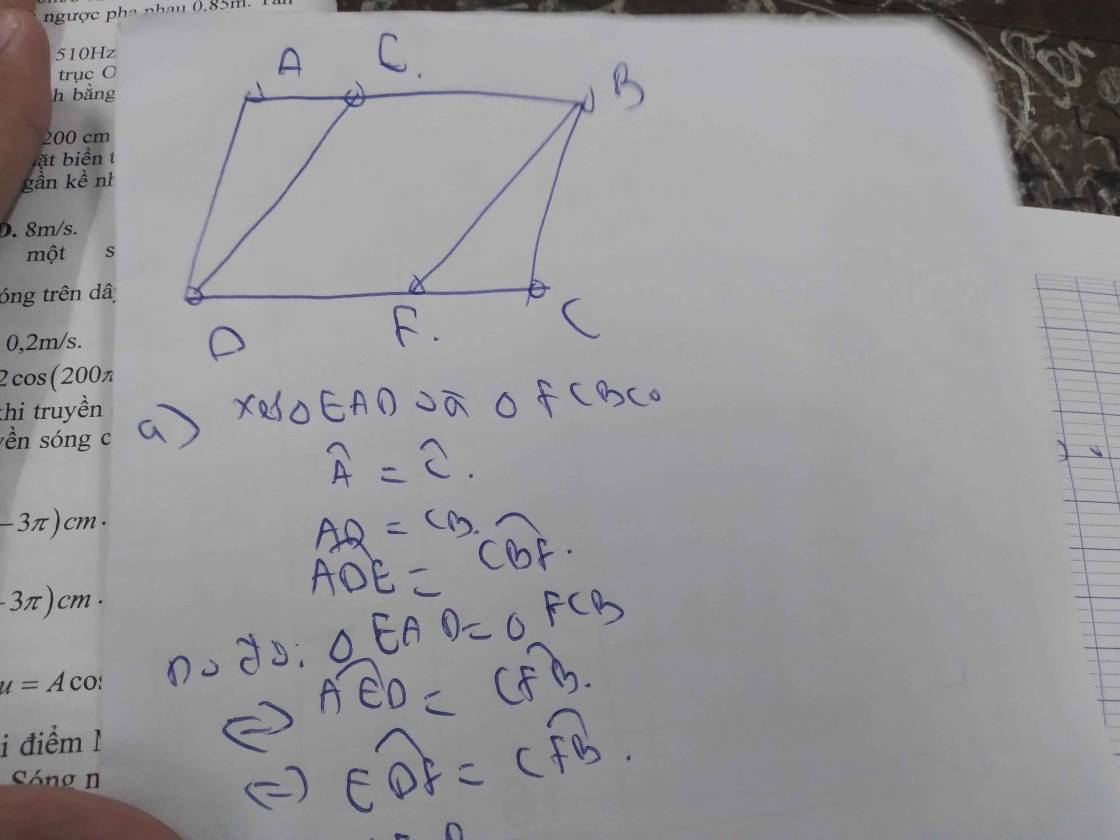
a: Xét ΔEAD và ΔFCB có
góc A=góc C
AD=CB
góc ADE=góc CBF(góc ADE=1/2*góc ADC=1/2*góc ABC=góc CBF)
Do đó; ΔEAD=ΔFCB
=>AE=CF
b: AE+EB=AB
CF+FD=CD
mà AB=CD và AE=CF
nên EB=FD
Xét tứ giác DEBF có
BE//FD
BE=FD
=>DEBF là hình bình hành
c: ABCD là hbh
=>AC cắt BD tại trung điểm của mỗi đường(1)
DEBF là hbh
=>DB cắt EF tại trung điểm của mỗi đường(2)
Từ (1), (2) suy ra AC,BD,EF đồng quy

Lời giải:
a) Theo tính chất đường phân giác ta có:
$\frac{BE}{ED}=\frac{AB}{AD}$
$\frac{AF}{FC}=\frac{AB}{BC}$
Mà $ABCD$ là hình bình hành nên $AD=BC\Rightarrow \frac{AB}{AD}=\frac{AB}{BC}$
$\Rightarrow \frac{BE}{ED}=\frac{AF}{FC}$ (đpcm)
b) Gọi O là giao điểm $AC,BD$. Ta có:
\(\frac{BE}{ED}=\frac{BD-ED}{ED}=\frac{2DO-ED}{ED}=\frac{2DO}{ED}-1\)
Tương tự: \(\frac{AF}{FC}=\frac{2OC}{FC}-1\)
Mà \(\frac{BE}{ED}=\frac{AF}{FC}\Rightarrow \frac{DO}{ED}=\frac{OC}{FC}\). Theo định lý Talet đảo suy ra $EF\parallel DC$ hay $EF\parallel AB$ (đpcm)

a: Xét ΔDAM và ΔBCN có
\(\widehat{D}=\widehat{B}\)
DA=BC
\(\widehat{DAM}=\widehat{BCN}\)
Do đó: ΔDAM=ΔBCN
Suy ra: AM=CN và DM=BN
Ta có: AN+NB=AB
CM+MD=CD
mà AB=CD
và DM=BN
nên AN=CM
Xét tứ giác AMCN có
AN//CM
AM//CN
Do đó: AMCN là hình bình hành