Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a) Theo tính chất đường phân giác ta có:
$\frac{BE}{ED}=\frac{AB}{AD}$
$\frac{AF}{FC}=\frac{AB}{BC}$
Mà $ABCD$ là hình bình hành nên $AD=BC\Rightarrow \frac{AB}{AD}=\frac{AB}{BC}$
$\Rightarrow \frac{BE}{ED}=\frac{AF}{FC}$ (đpcm)
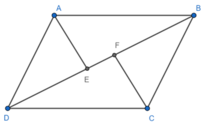
b) Gọi O là giao điểm $AC,BD$. Ta có:
\(\frac{BE}{ED}=\frac{BD-ED}{ED}=\frac{2DO-ED}{ED}=\frac{2DO}{ED}-1\)
Tương tự: \(\frac{AF}{FC}=\frac{2OC}{FC}-1\)
Mà \(\frac{BE}{ED}=\frac{AF}{FC}\Rightarrow \frac{DO}{ED}=\frac{OC}{FC}\). Theo định lý Talet đảo suy ra $EF\parallel DC$ hay $EF\parallel AB$ (đpcm)

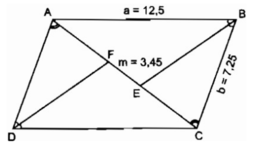
Vì ABCD là hình bình hành nên ∠ ABC = ∠ ADC.
Mặt khác, BE và DF lần lượt là phân giác của các góc B và D, do đó suy ra ∠ ADF = ∠ CBE
Mặt khác, ta có: AD = CB = b;
∠ DAF = ∠ BCE (so le trong)
Suy ra: △ ADF = △ CBE (g.c.g)
⇒ AF = CE
Đặt AF = CE = x
Theo tính chất của đường phân giác BE trong tam giác ABC, ta có: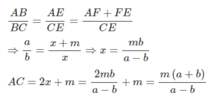
Thay số, tính trên máy tính điện tử cầm tay ta được: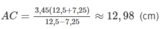

A B C D O
Xét tam giác ABC và BAD có :
AB : chung
\(\widehat{BAD}=\widehat{ABC}\)
AD = BC
( ABCD là hình thang cân )
\(\Rightarrow\Delta ABC=\Delta BAD\)
\(\Rightarrow\widehat{BAC}=\widehat{ABD}\)
\(\Delta AOB\)CÓ : \(\widehat{OAB}=\widehat{OBA}\Rightarrow\Delta AOB\)cân tại O nên OA = OB

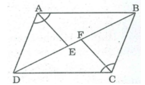
Ta có:
△ ABE = △ CDF (g.c.g) ⇒ S A B E = S C D F (l)
△ AED = △ CFB (g.c.g) ⇒ S A E D = S C F B (2)
Từ (1) và (2) ⇒ S A B E + S C F B = S C D F + S A E D
Hay S A B C F E = S A D C F E

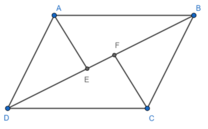
Ta có S A B C F E = S A B E + S B F C S A D C F E = S D F C + S D A E
Xét hình bình hàng ABCD có AE và CF lần lượt là phân giác của các góc A và C
nên suy ra: B A E ^ = D A E ^ = B C F ^ = D C F ^
Xét ΔABE và ΔDCF có:
AB = CD (gt), A B E ^ = C D F ^ (slt), B A E ^ = D C F ^ (cmt)
=> ΔABE = ΔDCF (g.c.g)
=> SABE = SCDF (1)
Xét ΔBCF và ΔDAE có:
AD = BC (gt), A D E ^ = C B F ^ (slt), D A E ^ = B C F ^ (cmt)
=> ΔBCF = ΔDAE (g.c.g)
=> SBCF = SDAE (2)
Từ (1) và (2) suy ra:
SABE + SBCF = SCDF + SDAE
=> SABCFE = SADCFE
Đáp án cần chọn là: C