K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
3 tháng 8 2021
a) 1030 và 2100 .
1030 = ( 103 )10 = 100010 .
2100 = ( 210 )10 = 102410 .
Vì 100010 < 102410 .
\(\Rightarrow\) 1030 < 2100 .
Vậy ....
b) \(\uparrow\) Lm như trên .
22 tháng 1
Sửa đề: \(S=2^{100}-2^{99}+2^{98}-...+2^2-2\)
=>\(2\cdot S=2^{101}-2^{100}+2^{99}-...+2^3-2^2\)
=>\(2S+S=2^{100}-2^{99}+2^{98}-...+2^2-2+2^{101}-2^{100}+2^{99}-...+2^3-2^2\)
=>\(3S=2^{101}-2\)
=>\(S=\dfrac{2^{101}-2}{3}\)
N
1 tháng 11 2018
\(3x=7y\Rightarrow\frac{x}{7}=\frac{y}{3}\)
đặt \(k=\frac{x}{7}=\frac{y}{3}\Rightarrow x=7k,y=3k\)
\(\Rightarrow xy=7k.3k=21k^2=2100\Rightarrow k^2=100\Rightarrow\orbr{\begin{cases}k=10\\k=-10\end{cases}}\)
\(k=10\Rightarrow x=70,y=30\)
\(k=-10\Rightarrow x=-70,y=-30\)
Vậy x=70 và y=30, x=-70 và y=-30
NV
1 tháng 11 2018
\(3x=7y\)
\(\Leftrightarrow\frac{x}{7}=\frac{y}{3}\)
\(\Leftrightarrow\frac{x^2}{49}=\frac{xy}{21}=\frac{y^2}{9}\)
\(\Leftrightarrow\frac{x^2}{49}=\frac{y^2}{9}=\frac{2100}{21}=100\)
\(\Leftrightarrow\hept{\begin{cases}\frac{x^2}{49}=100\\\frac{y^2}{9}=100\end{cases}\Leftrightarrow\hept{\begin{cases}x^2=4900\\y^2=900\end{cases}}}\Leftrightarrow\hept{\begin{cases}x=\pm70\\y=\pm30\end{cases}}\)
Vậy \(\left(x,y\right)\in\left\{\left(-70,-30\right);\left(70,30\right)\right\}\)
!!!
G
10 tháng 11 2016
\(9^{1575}=\left(3^2\right)^{1575}=3^{3150}\)
UCLN(3150,2100) = 1050. Đưa các lũy thừa cần so sánh về cùng số mũ 1050 như sau:
\(3^{3150}=\left(3^3\right)^{1050}=27^{1050}\)
\(5^{2100}=\left(5^2\right)^{1050}=25^{1050}\)
Do \(27^{1050}>25^{1050}\) Suy ra \(9^{1575}>5^{2100}\)
TD
1
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
14 tháng 5 2022
\(A.x=x+x^2+x^3+...+x^{101}\)
\(A.x-A=x^{101}-1\Rightarrow A\left(x-1\right)=x^{101}-1\)
\(\Rightarrow A=\dfrac{x^{101}-1}{x-1}\)
MC
4 tháng 1 2019
\(S=1+2+2^2+2^3+...+2^{100}\)
\(\Rightarrow2S=2+2^2+2^3+2^4+...+2^{101}\)
\(\Rightarrow2S-S=\left(2+2^2+2^3+...+2^{101}\right)-\left(1+2+2^2+...+2^{100}\right)\)
\(\Rightarrow S=2^{101}-1\)
Vậy \(S=2^{101}-1\)
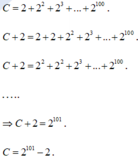
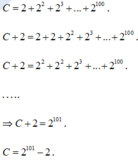
Nếu rảnh thì lấy giấy nháp ra tính:)
calculator :)