Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(V_{SABC}=\dfrac{1}{3}SA.\dfrac{1}{2}AB.AC=\dfrac{a^3\sqrt{3}}{6}\)
\(S_{SAM}=\dfrac{1}{2}S_{SAB}\Rightarrow V_{SAMC}=\dfrac{1}{2}V_{SABC}=\dfrac{a^3\sqrt{3}}{12}\)
Tam giác SAB vuông tại A nên AM là trung tuyến ứng với cạnh huyền
\(\Rightarrow AM=\dfrac{1}{2}SB=\dfrac{1}{2}\sqrt{SA^2+AB^2}=a\)
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp AC\\AC\perp AB\end{matrix}\right.\) \(\Rightarrow AC\perp\left(SAB\right)\Rightarrow AC\perp AM\)
Hay tam giác ACM vuông tại M
\(\Rightarrow S_{AMC}=\dfrac{1}{2}AM.AC=\dfrac{a^2}{2}\)
\(\Rightarrow d\left(S;\left(AMC\right)\right)=\dfrac{3V_{SAMC}}{S_{AMC}}=\dfrac{a\sqrt{3}}{2}\)

Kẻ \(MH\perp CD\Rightarrow AMHD\) là hcn
\(\Rightarrow MH=AD=a\)
\(V_{SDCM}=\dfrac{1}{3}SA.S_{MCD}=\dfrac{1}{3}SA.\dfrac{1}{2}MH.CD=\dfrac{1}{6}.a.a.2a=\dfrac{a^3}{3}\)
b.
Trong tam giác vuông DAM, kẻ \(AE\perp DM\Rightarrow DM\perp\left(SAE\right)\)
\(\Rightarrow\widehat{SEA}\) là góc giữa (SDM) và đáy hay \(\widehat{SEA}=60^0\)
\(\Rightarrow AE=\dfrac{SA}{tan60^0}=\dfrac{a\sqrt{3}}{3}\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{AE^2}=\dfrac{1}{AM^2}+\dfrac{1}{AD^2}\Rightarrow AM=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow V_{SADM}=\dfrac{1}{3}AM.\dfrac{1}{2}SA.AD=\dfrac{a^3\sqrt{2}}{12}\)
Kẻ \(AF\perp SE\Rightarrow AF\perp\left(SDM\right)\Rightarrow AF=d\left(A;\left(SDM\right)\right)\)
\(\dfrac{1}{AF^2}=\dfrac{1}{SA^2}+\dfrac{1}{AE^2}\Rightarrow AF=\dfrac{a}{2}\)


Gọi cạnh của tứ diện đều ABCD là a thì cạnh của hình bát diện đều (H) là \(\dfrac{a}{2}\). Khi đó :
\(V_{ABCD}=a^3\dfrac{\sqrt{2}}{12};V_{\left(H\right)}=\dfrac{1}{3}\left(\dfrac{a}{2}\right)^3\sqrt{2}=a^3\dfrac{\sqrt{2}}{24}\)
Từ đó suy ra :
\(\dfrac{V_{\left(H\right)}}{V_{ }ABCD}=\dfrac{1}{2}\)

\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(AC=a\sqrt{2}\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=\dfrac{\sqrt{3}}{3}\)
\(\Rightarrow\widehat{SCA}=30^0\)


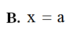
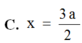
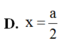

1.
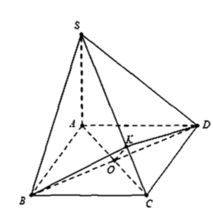
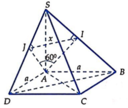
Gọi $I$ là trung điểm $AB$ thì do tam giác $DAB$ và $CAB$ cân tại $D$ và $C$ nên:
$DI\perp AB; CI\perp AB$
$\Rightarrow (DCI)\perp AB$
$\Rightarrow (DCI)\perp AI$ và $(DCI)\perp BI$
Do đó:
\(V_{ABCD}=V_{DAIC}+V_{DIBC}=\frac{1}{3}AI.S_{DIC}+\frac{1}{3}BI.S_{DIC}\)
\(=\frac{1}{3}S_{DIC}(AI+BI)=\frac{1}{3}S_{DIC}.AB=\frac{x}{3}S_{DIC}\)
\(DI=\sqrt{DA^2-AI^2}=\sqrt{DA^2-(\frac{AB}{2})^2}=\sqrt{12-\frac{x^2}{4}}\)
\(CI=\sqrt{AC^2-AI^2}=\sqrt{AC^2-(\frac{AB}{2})^2}=\sqrt{12-\frac{x^2}{4}}\)
$\Rightarrow DCI$ là tam giác cân tại $I$
Kẻ $IM\perp DC$ thì $M$ là trung điểm $DC$
$IM=\sqrt{DI^2-DM^2}=\sqrt{12-\frac{x^2}{4}-(\sqrt{3})^2}$
$=\sqrt{9-\frac{x^2}{4}}$
\(S_{DIC}=\frac{IM.DC}{2}=\sqrt{9-\frac{x^2}{4}}.2\sqrt{3}:2=\frac{\sqrt{3}.\sqrt{36-x^2}}{2}\)
Vậy: \(V_{ABCD}=\frac{\sqrt{3}}{6}x\sqrt{36-x^2}=\frac{\sqrt{3}}{6}\sqrt{x^2(36-x^2)}\)
\(\leq \frac{\sqrt{3}}{6}.\frac{x^2+36-x^2}{2}=3\sqrt{3}\) theo BĐT Cô-si
Vậy $V_{ABCD}$ max bằng $3\sqrt{3}$ khi $x^2=36-x^2$
$\Leftrightarrow x=3\sqrt{2}$
Hình bài 1