Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là B
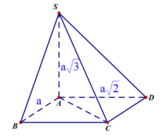
Vì SA vuông góc với đáy nên góc φ giữa SC và mặt phẳng (ABCD) bằng góc giữa SC và hình chiếu AC của nó lên đáy. Suy ra φ = S C A ^ (vì S C A ^ là góc nhọn trong tam giác vuông SAC)
Trong hình chữ nhật ABCD, ta có AC=a 3 . Suy ra tam giác SAC vuông cân ở A.
![]()
Vậy, số đo của góc giữa SC và mặt phẳng (ABCD) bằng 450

Chọn A.
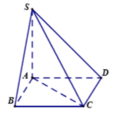
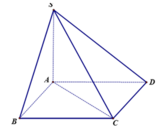
Vì SA vuông góc với đáy nên góc (SC,(ABCD)) = SCA.
Trong hình vuông ABCD có: AC = a 2 theo giả thiết, SA = a 2 => tam giác SAC vuông cân tại A
=> góc SCA = 45 °

Chọn D.
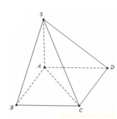
Vì S A ⊥ ( A B C D ) nên AC là hình chiếu vuông góc của SC lên(ABCD).
Góc giữa giữa SC và mp (ABCD) bằng góc SC&AC ⇒ α = SCA.
Xét tam giác SAC vuông tại A có
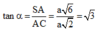
⇒ α = 60 o


Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
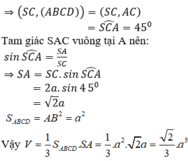

Chọn đáp án A
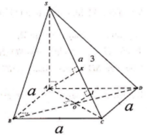
Gọi ![]()
Ta có: ![]()
Mặt khác ![]()
=> OI là đường vuông góc chung.
=> d(BD;SC) = OI
Kẻ ![]()
OI là đường trung bình của tam giác AKC.
![]()
Ta có: ![]()
![]()
![]()
Xét tam giác SAC vuông tại A: 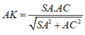

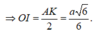
Vậy khoảng cách giữa BD và SC bằng a 6 6

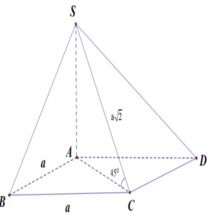
Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
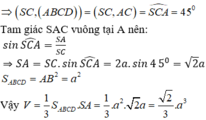

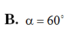
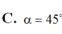
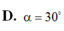

\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(AC=a\sqrt{2}\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=\dfrac{\sqrt{3}}{3}\)
\(\Rightarrow\widehat{SCA}=30^0\)