Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

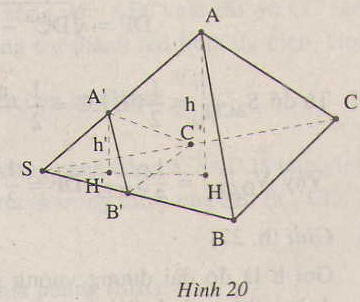
Gọi h và h’ lần lượt là chiều cao hạ từ A, A’ đến mặt phẳng (SBC).
Gọi S1 và S2 theo thứ tự là diện tích các tam giác SBC và SB’C’.
Khi đó ta có h′h=SA′SAh′h=SA′SA và 12B′SC′.SB′.SC′12BSC.SB.SC=SB′SB.SC′SC12B′SC′.SB′.SC′12BSC.SB.SC=SB′SB.SC′SC
Suy ra VS.A′B′C′VS.ABC=VA′.SB′C′VA.SBC=13h′S213hS1=SA′SA⋅SB′SB⋅SC′SCVS.A′B′C′VS.ABC=VA′.SB′C′VA.SBC=13h′S213hS1=SA′SA⋅SB′SB⋅SC′SC
Đó là điều phải chứng minh.

Chắc là mp (P) đi qua A'
Đặt \(V_{SABCD}=V\)
Theo định lý Talet: \(\dfrac{SA'}{SA}=\dfrac{SB'}{SB}=\dfrac{SC'}{SC}=\dfrac{SD'}{SD}=\dfrac{3}{4}\)
Ta có: \(\dfrac{V_{SA'B'C'D'}}{V_{SABCD}}=\dfrac{2V_{SA'B'C'}}{2V_{SABC}}=\dfrac{V_{SA'B'C'}}{V_{SABC}}=\dfrac{SA'}{SA}.\dfrac{SB'}{SB}.\dfrac{SC'}{SC}=\dfrac{3}{4}.\dfrac{3}{4}.\dfrac{3}{4}=\dfrac{27}{64}\)
Tỉ số thể tích 2 phần (phần trên chia phần dưới) là: \(\dfrac{27}{64}:\left(1-\dfrac{27}{64}\right)=\dfrac{27}{37}\)

\(\dfrac{V_{SAHKE}}{V_{SABCD}}=\dfrac{2V_{SAHK}}{2V_{SABC}}=\dfrac{V_{SAHK}}{V_{SABC}}\)
\(V_{SABC}=\dfrac{1}{3}SA.\dfrac{1}{2}AB.BC=\dfrac{a^3}{3}\); \(V_{SABCD}=\dfrac{2a^3}{3}\)
\(\dfrac{SH}{SB}=\dfrac{SA^2}{SB}:SB=\left(\dfrac{SA}{SB}\right)^2\); \(\dfrac{SK}{SC}=\dfrac{SA^2}{SC}:SC=\left(\dfrac{SA}{SC}\right)^2\)
\(SB=\sqrt{SA^2+AB^2}=a\sqrt{5}\) ; \(SC=\sqrt{SA^2+AC^2}=a\sqrt{6}\)
\(\dfrac{V_{SAHK}}{V_{SABC}}=\left(\dfrac{SA}{SB}\right)^2.\left(\dfrac{SA}{SC}\right)^2\)
\(\Rightarrow V_{SAHKE}=\left(\dfrac{2a}{a\sqrt{5}}\right)^2.\left(\dfrac{2a}{a\sqrt{6}}\right)^2.\dfrac{2a^3}{3}=\dfrac{16a^3}{45}\)

Do \(SA=SB=SC=SD\) và đáy là hình vuông nên \(SABCD\) là chóp đều
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\)
Theo tính đối xứng của chóp đều \(\Rightarrow SB'=SD'\Rightarrow B'D'||BD\)
Gọi M là giao điểm SO và AC' \(\Rightarrow M\in B'D'\) (t/c giao tuyến 3 mp cắt nhau)
Áp dụng định lý Talet:
\(\dfrac{SM}{SO}=\dfrac{SD'}{SD}=\dfrac{SB'}{SB}=\dfrac{2}{3}\Rightarrow M\) là trọng tâm tam giác SAC
\(\Rightarrow C'\) là trung điểm SC \(\Rightarrow\dfrac{SC'}{SC}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{V_{SAB'C'D'}}{V_{SABCD}}=\dfrac{2V_{SAB'C'}}{2V_{SABC}}=\dfrac{V_{SAB'C'}}{V_{SABC}}=\dfrac{SA}{SA}.\dfrac{SB'}{SB}.\dfrac{SC'}{SC}=1.\dfrac{2}{3}.\dfrac{1}{2}=\dfrac{1}{3}\)

1.
Gọi $I$ là trung điểm $AB$ thì do tam giác $DAB$ và $CAB$ cân tại $D$ và $C$ nên:
$DI\perp AB; CI\perp AB$
$\Rightarrow (DCI)\perp AB$
$\Rightarrow (DCI)\perp AI$ và $(DCI)\perp BI$
Do đó:
\(V_{ABCD}=V_{DAIC}+V_{DIBC}=\frac{1}{3}AI.S_{DIC}+\frac{1}{3}BI.S_{DIC}\)
\(=\frac{1}{3}S_{DIC}(AI+BI)=\frac{1}{3}S_{DIC}.AB=\frac{x}{3}S_{DIC}\)
\(DI=\sqrt{DA^2-AI^2}=\sqrt{DA^2-(\frac{AB}{2})^2}=\sqrt{12-\frac{x^2}{4}}\)
\(CI=\sqrt{AC^2-AI^2}=\sqrt{AC^2-(\frac{AB}{2})^2}=\sqrt{12-\frac{x^2}{4}}\)
$\Rightarrow DCI$ là tam giác cân tại $I$
Kẻ $IM\perp DC$ thì $M$ là trung điểm $DC$
$IM=\sqrt{DI^2-DM^2}=\sqrt{12-\frac{x^2}{4}-(\sqrt{3})^2}$
$=\sqrt{9-\frac{x^2}{4}}$
\(S_{DIC}=\frac{IM.DC}{2}=\sqrt{9-\frac{x^2}{4}}.2\sqrt{3}:2=\frac{\sqrt{3}.\sqrt{36-x^2}}{2}\)
Vậy: \(V_{ABCD}=\frac{\sqrt{3}}{6}x\sqrt{36-x^2}=\frac{\sqrt{3}}{6}\sqrt{x^2(36-x^2)}\)
\(\leq \frac{\sqrt{3}}{6}.\frac{x^2+36-x^2}{2}=3\sqrt{3}\) theo BĐT Cô-si
Vậy $V_{ABCD}$ max bằng $3\sqrt{3}$ khi $x^2=36-x^2$
$\Leftrightarrow x=3\sqrt{2}$