PT
16
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
A
1
DM
0
TN
26 tháng 5 2017
\(=\frac{25}{4}-\left(x-\frac{1}{2}\right)^2\) xuống lớp 7 học đi nhé
26 tháng 5 2017
GTLN \(-x^2\)+\(x\)+\(6\)=\(-\left(x^2-x-6\right)\)
=\(-\left(x^2-2.\frac{1}{2}x+\frac{1}{4}-\frac{1}{4}-6\right)\)=\(-\left(x-\frac{1}{2}\right)^2-\frac{25}{4}\)
=\(\left(x-\frac{1}{2}\right)^2+\frac{25}{4}\)
Vì \(\left(x-\frac{1}{2}\right)^2\)\(\ge\)\(0\)Nên \(\left(x-\frac{1}{2}\right)^2+\frac{25}{4}\)\(\ge0\)
Vậy GTLN của biểu thức là \(\frac{25}{4}\)khi \(x=\frac{1}{2}\)
19 tháng 5 2022
a: Đường thẳng Ox có phương trình tổng quát là:
0x+y+0=0
=>y=0x+0
Để Ox//(d) thì m-1=0 và n<>0
=>m=1 và n<>0
b: Vì hệ số góc là -3 nên m-1=-3
hay m=-2
Vậy: (d): y=-3x+n
Thay x=1 và y=-1 vào (d), ta được:
n-3=-1
hay n=2
17 tháng 4 2017
Gọi lượng nước vòi 1 và vòi 2 chảy vào bể trong 1 giờ là x, y (bể)
Hai vòi cùng chảy thì 3h đầy: \(3x+3y=1\left(1\right)\)
Thời gian để vòi 1 chảy nửa bể: \(\frac{1}{2x}\left(h\right)\)
Thời gian để vòi 2 chảy nửa bể: \(\frac{1}{2y}\left(h\right)\)
\(\Rightarrow\frac{1}{2x}+\frac{1}{2y}=8\left(2\right)\)
Từ (1) và (2) ta có hệ: \(\hept{\begin{cases}3x+3y=1\\\frac{1}{2x}+\frac{1}{2y}=8\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=\frac{1}{4}\\y=\frac{1}{12}\end{cases}}\) hoặc \(\hept{\begin{cases}x=\frac{1}{12}\\y=\frac{1}{4}\end{cases}}\)
Vậy nếu 1 vòi chảy thì vòi 1 chảy trong 4 h hoặc 12 h, vòi 2 chảy trong 12 h hoặc 4 h
WR
23 tháng 6 2019
Đkxđ: \(\hept{\begin{cases}x\ge-\frac{1}{4}\\y\ge2\end{cases}}\)
\(\Leftrightarrow2+\sqrt{\left(\sqrt{x+\frac{1}{4}}+\frac{1}{2}\right)^2}=y\Leftrightarrow2+\frac{1}{2}+\sqrt{x+\frac{1}{2}}=y\Leftrightarrow\sqrt{x+\frac{1}{2}}+\frac{5}{2}=y\)
do x,y nguyên dương nên \(\sqrt{x+\frac{1}{2}}+\frac{5}{2}\)nguyên dương\(\Leftrightarrow\sqrt{x+\frac{1}{2}}=\frac{k}{2}\)(K là số nguyên lẻ, \(k>1\))
\(\Rightarrow x=\frac{k^2-2}{4}\)
do \(k^2\)là số chính phương chia 4 dư 0,1 \(\Rightarrow x=\frac{k^2-2}{4}\notin Z\)
=> ko tồn tại cặp số nguyên dương x,y tmđkđb
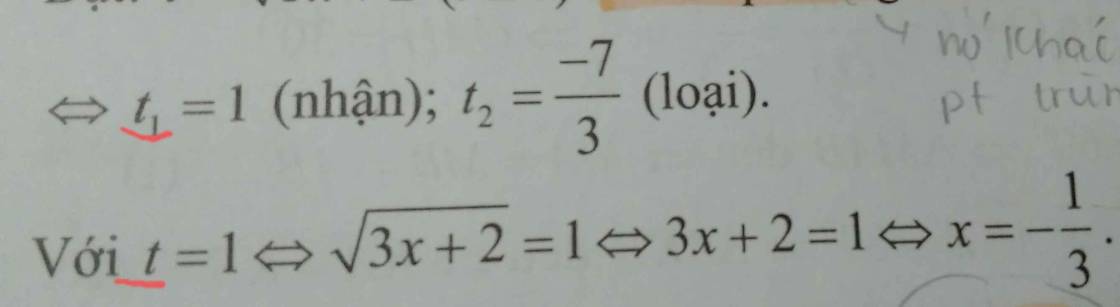
1+1=2 nha bn