Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: D
( v ì x ≥ - 7 v à x 2 + 6 x – 16 ≠ 0 < = > x ≠ - 8 v à x ≠ 2 )

a) TXĐ: \(D=R\).
b) \(TXD=D=R\backslash\left\{4\right\}\)
c) Đkxđ: \(\left\{{}\begin{matrix}4x+1\ge0\\-2x+1\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{-1}{4}\\x\le\dfrac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow\dfrac{-1}{4}\le x\le\dfrac{1}{2}\).
TXĐ: D = \(\left[\dfrac{-1}{4};\dfrac{1}{2}\right]\)
a) Đkxđ: \(\left\{{}\begin{matrix}x+9\ge0\\x^2+8x-20\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge-9\\\left\{{}\begin{matrix}x\ne2\\x\ne-10\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-9\\x\ne2\end{matrix}\right.\)
Txđ: D = [ - 9; 2) \(\cup\) \(\left(2;+\infty\right)\)
b) Đkxđ: \(\left\{{}\begin{matrix}2x+1\ne0\\x-3\ne0\end{matrix}\right.\Leftrightarrow\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{-1}{2}\\x\ne3\end{matrix}\right.\)
Txđ: \(D=R\backslash\left\{\dfrac{-1}{2};3\right\}\)
c) \(x^2+2x-5\ne0\Leftrightarrow\left\{{}\begin{matrix}x\ne-1+\sqrt{6}\\x\ne-1-\sqrt{6}\end{matrix}\right.\)
Txđ: \(D=R\backslash\left\{-1+\sqrt{6};-1-\sqrt{6}\right\}\)

Ta có:
Tập hợp A:
\(A=\left\{1;2;3;4;5\right\}\)
Tập hợp B:
\(B=\left\{4;5;6;7\right\}\)
Mà: T = A \ B
\(\Rightarrow T=\left\{1;2;3\right\}\)
⇒ Chọn A

Ta có:
Tập hợp A:
\(A=\left\{1;3;5;7;9\right\}\)
Tập hợp B:
\(B=\left\{0;1;2;4;5;6;8\right\}\)
Mà: \(C=A\cup B\)
\(\Rightarrow C=\left\{0;1;2;3;4;5;6;7;8;9\right\}\)
⇒ Chọn D

a) Biểu thức \(f(x)\) có nghĩa khi và chỉ khi \(2x + 7 \ge 0,\)tức là khi \(x \ge \frac{{ - 7}}{2}.\)
Vậy tập xác định của hàm số này là \(D = \left[ { - \frac{7}{2}; + \infty )} \right.\)
b) Biểu thức \(f(x)\) có nghĩa khi và chỉ khi \({x^2} - 3x + 2 \ne 0,\)tức là khi \(x \ne 2,x \ne 1.\)
Vậy tập xác định của hàm số này là \(D = \mathbb{R}\backslash \left\{ {1;2} \right\}\)


Vì 4 đồ thị hàm số cắt trục tung tại 4 điểm phân biệt nên ta chỉ cần xác định tọa độ giao điểm của mỗi hàm số với trục tung là có thể phân biệt 4 đồ thị hàm số.
Đồ thị hàm số \(({P_1}):y = - 2{x^2} - 4x + 2\) cắt trục tung tại điểm có tung độ bằng 2, tức là đồ thị đi qua điểm có tọa độ (0; 2) => Đồ thị là đường màu xanh lá.
Đồ thị hàm số \(({P_2}):y = 3{x^2} - 6x + 5;\) cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5) => Đồ thị là đường màu xanh dương.
Đồ thị hàm số \(({P_3}):y = 4{x^2} - 8x + 7;\) cắt trục tung tại điểm có tung độ bằng 7, tức là đồ thị đi qua điểm có tọa độ (0; 7) => Đồ thị là đường màu nâu đỏ.
Đồ thị hàm số \(({P_4}):y = - 3{x^2} - 6x - 1\) cắt trục tung tại điểm có tung độ bằng -1, tức là đồ thị đi qua điểm có tọa độ (0; -1) => Đồ thị là đường màu vàng.
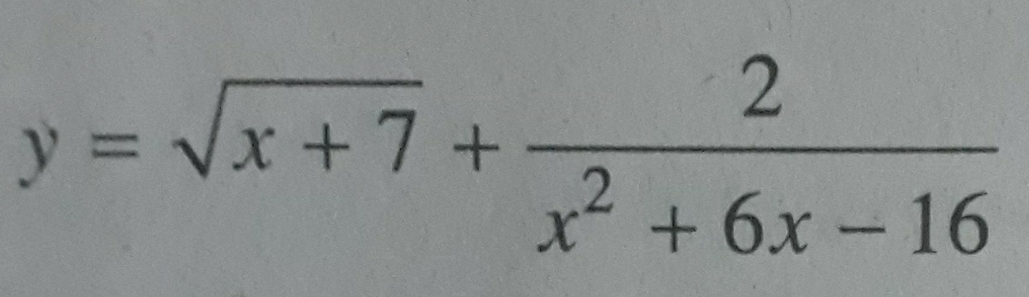

1.Ý C
Hàm số có nghĩa khi \(x^2+14x+45\ne0\Leftrightarrow x\ne\left\{-5;-9\right\}\)
\(\Rightarrow D=R\backslash\left\{-5;-9\right\}\)
2. Ý D
Hàm số có nghĩa khi \(\left\{{}\begin{matrix}x+7\ge0\\x^2+6x-16\ne0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x\ge-7\\x\ne\left\{2;-8\right\}\end{matrix}\right.\)
\(\Rightarrow D=\)\([-7;+ \infty) \)\(\backslash\left\{2\right\}\)
ĐK : \(x^2+14x+45\ne0\)
\(\Leftrightarrow\hept{\begin{cases}x\ne-5\\x\ne-9\end{cases}}\)
\(TXĐ:D=R\backslash\left\{-5;-9\right\}\)
Chọn C