33.22-32.19
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VN
Võ Ngọc Phương
VIP
13 tháng 11 2023
\(\left\{210:\left[16+3.\left(6+3.2^2\right)\right]\right\}-3\)
\(=\left\{210:\left[16+3.\left(6+3.4\right)\right]\right\}-3\)
\(=\left\{210:\left[16+3.\left(6+12\right)\right]\right\}-3\)
\(=\left\{210:\left[16+3.18\right]\right\}-3\)
\(=\left\{210:\left[16+54\right]\right\}-3\)
\(=\left\{210:70\right\}-3\)
\(=3-3\)
\(=0\)
NN
1
HQ
Hà Quang Minh
Giáo viên
15 tháng 8 2023
\(a,23\cdot125+78\cdot125-125\\ =125\cdot\left(23+78-1\right)\\ =125\cdot100\\ =12500\\ b,37\cdot46+18\cdot54-17\cdot46+54\cdot2\\ =46\cdot\left(37-17\right)+54\cdot\left(18+2\right)\\ =46\cdot20+54\cdot20\\ =20\cdot\left(46+54\right)\\ =20\cdot100\\ =2000\\ b,3\cdot2^2-2^3:2+2^2\\ =3\cdot4-4+4\\ =12\\ d,7^3\cdot9+3^2\cdot7^4\\ =7^3\cdot9+7^4\cdot9\\ =7^3\cdot9\cdot\left(1+7\right)\\ =343\cdot9\cdot8\\ =24696\)
H9
HT.Phong (9A5)
CTVHS
15 tháng 8 2023
a) \(23\cdot125+78\cdot125-125\)
\(=125\cdot\left(23+78-1\right)\)
\(=125\cdot100\)
\(=12500\)
b) \(37\cdot46+18\cdot54-17\cdot46+54\cdot2\)
\(=54\cdot\left(18+2\right)+46\cdot\left(37-17\right)\)
\(=54\cdot20+46\cdot20\)
\(=54\cdot\left(20+46\right)\)
\(=20\cdot100\)
\(=2000\)
c) \(3\cdot2^2-2^3:2+2^2\)
\(=3\cdot2^2-2^2+2^2\)
\(=3\cdot2^2\)
\(=3\cdot4\)
\(=12\)
d) \(7^3\cdot9+3^2\cdot7^4\)
\(=7^3\cdot3^2+3^2\cdot7^4\)
\(=7^3\cdot3^2\cdot\left(1+7\right)\)
\(=24696\)
15 tháng 8 2023
a) 23.125+78.125-125
= (23+78-1).125
= 100.125
= 12500
b) 37.46+18.54-17.46+54.2
= (37-17).46+(18+2).54
= 20.46+20.54
= 20.(46+54)
= 20.100
= 2000
c) 3.22-23:2+22
= 3.22-22+22
= 3.22
= 3.4
= 12
d) 73.9+32.74-45.539
= 73.9+9.74-5.9.72.11
= 9.(73+74)-5.9.72.11
=9.2744-9.2695
= 9.(2744-2695)
= 9.49
= 441
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
15 tháng 8 2023
a/
=125(23+78-1)=125.100=12500
b/
=46(37-17)+54(18+2)
=20(46+54)=20.100=2000
c/
=3.22-22+22=3.4=12
d/
=73.32+32.74-5.32.72.11=
=32.72(7+72-55)=32.72=441
23 tháng 8 2017
Ta có:\(x\left(x+y\right)+y\left(x-y\right)=x^2+xy+xy-y^2\)
\(=x^2+2xy-y^2\)
\(=-\left(x^2-2xy+y^2\right)+2x^2\)
Áp dụng hằng đẳng thức (a-b)2=a2-2ab+b2 ta đc:
\(=2x^2-\left(x-y\right)^2\)
Tại x = - 8 ; y = 7 ta đc:
\(=2\left(-8\right)^2-\left(-8-7\right)^2\)
\(=-241\)
6 tháng 12 2023
1: \(23+\left(-13\right)+\left(-50\right)\)
\(=23-13-50\)
=10-50
=-40
2: \(-5+15+\left(-123\right)\)
\(=\left(-5+15\right)-123\)
=10-123
=-113
3: \(5871:\left\{928-\left[\left(-82+247\right)\right]\right\}\cdot5\)
\(=5871-\left\{928+82-247\right\}\cdot5\)
\(=5871-763\cdot5=5871-3815=2056\)
4: \(40-\left(4\cdot5^2-3\cdot2^3\right)\)
\(=40-4\cdot5^2+3\cdot2^3\)
\(=40-4\cdot25+3\cdot8\)
=40-100+24
=64-100
=-36
5: \(6^2\cdot5-7^2+149\)
\(=36\cdot5-49+149\)
\(=180+149-49\)
=180+100
=280
6: \(-210:\left[16+3\cdot\left(6+3\cdot2^2\right)\right]+\left(-2022\right)\)
\(=-210:\left[16+3\cdot\left(6+3\cdot4\right)\right]+\left(-2022\right)\)
\(=-210:\left[16+3\cdot18\right]+\left(-2022\right)\)
\(=-210:70-2022\)
=-3-2022
=-2025
7: \(5\cdot2^3+7^{11}:7^9-2023^0\cdot1^8\)
\(=5\cdot8+7^2-1\)
=40+49-1
=39+49
=88
8: \(400:\left\{5\cdot\left[360-\left(290+2\cdot5^2\right)\right]\right\}\)
\(=400:\left\{5\cdot\left[360-290-2\cdot25\right]\right\}\)
\(=400:\left\{5\cdot20\right\}\)
\(=\dfrac{400}{100}=4\)
9: \(75-\left(3\cdot5^2\right)-4\cdot5^3\)
\(=75-3\cdot25-4\cdot5^3\)
=-4*125
=-500
CM
6 tháng 12 2017
Cho x = 0 => y = √3 ta được (0; √3).
Cho y = 0 => √3 x + √3 = 0 => x = -1 ta được (-1; 0).
Như vậy để vẽ được đồ thị hàm số y = √3 x + √3 ta phải xác định được điểm √3 trên Oy.
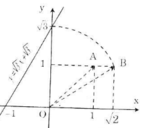
Các bước vẽ đồ thị y = √3 x + √3 :
+ Dựng điểm A(1; 1) được OA = √2.
+ Dựng điểm biểu diễn √2 trên Ox: Quay một cung tâm O, bán kính OA cắt tia Ox, được điểm biểu diễn √2.
+ Dựng điểm B(√2; 1) được OB = √3.
+ Dựng điểm biểu diễn √2. Trên trục Oy: Quay một cung tâm O, bán kính OB cắt tia Oy, được điểm biểu diễn √3
+ Vẽ đường thẳng qua điểm biểu diễn √3 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √3 x + √3.
b) Áp dụng vẽ đồ thị hàm số y = √5 x + √5
- Cho x = 0 => y = √5 ta được (0; √5).
- Cho y = 0 => √5 x + √5 = 0 => x = -1 ta được (-1; 0).
Ta phải tìm điểm trên trục tung có tung độ bằng √5.
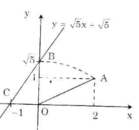
Cách vẽ:
+ Dựng điểm A(2; 1) ta được OA = √5.
+ Dựng điểm biểu diễn √5 trên trục Oy. Quay một cung tâm O, bán kính OA cắt tia Oy, được điểm biểu diễn √5. Vẽ đường thẳng qua điểm biểu diễn √5 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √5 x + √5.
`3^3 . 22 - 3^2 . 19`
`= 27 . 22 - 9 . 19`
`= 594 -171`
`= 423`