giúp mk với
giải hệ phương trình:
x3=3x+8y
y3=3y+8x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 9 2019
x 3 = 3 x + 8 y ( 1 ) y 3 = 3 y + 8 x ( 2 )
Lấy (1) trừ (2) vế trừ vế ta được:;
x 3 - y 3 = 3 x + 8 y - 3 y + 8 x ⇔ x - y . x 2 + x y + y 2 = - 5 x + 5 y ⇔ x - y . x 2 + x y + y 2 + 5 x - 5 y = 0 ⇔ x - y . x 2 + x y + y 2 + 5 x - y = 0 ⇔ x - y x 2 + x y + y 2 + 5 = 0 ⇔ [ x - y = 0 x 2 + x y + y 2 + 5 = 0
* Nếu x- y = 0 hai x = y thay vào (1)ta được: x 3 = 3x + 8x
⇔ x 3 = 11 x ⇔ x 3 - 11 x = 0 ⇔ [ x = 0 ⇒ y = 0 x = 11 ⇒ y = 11 x = - 11 ⇒ y = - 11
*Nếu x 2 + x y + y 2 + 5 = 0 ⇔ x 2 + 2 . 1 2 y + y 2 4 + 3 y 2 4 + 5 = 0
⇔ x + y 2 2 + 3 y 2 4 + 5 = 0 (vô lí).
Vậy phương trình đã cho có 3 nghiệm là: 0 ; 0 , 11 ; 11 ; - 11 ; - 11
Chọn C.
CM
11 tháng 6 2017
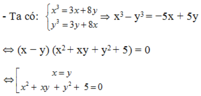
Khi x = y thì x 3 = 11 x = 0 ⇔ x = 0 ; x = ± 11
Khi x 2 + x y + y 2 + 5 = 0 ⇔ x + 1 2 y 2 + 3 4 y 2 + 5 = 0 (phương trình vô nghiệm)
Vậy hệ có nghiệm − 11 ; − 11 ; 11 ; 11
Đáp án cần chọn là: A
11 tháng 12 2020
Ta có: \(\left\{{}\begin{matrix}x^3=3x+8y\\y^3=8x+3y\end{matrix}\right.\)
\(\Rightarrow x^3-y^3=5y-5x\)\(\Leftrightarrow x^3-y^3+5x-5y=0\)\(\Leftrightarrow\left(x-y\right)\left(x^2+xy+y^2+5\right)=0\)
\(\Leftrightarrow x=y\)(vì \(x^2+xy+y^2+5>0\))
Thay \(x=y\) vào phương trình \(x^3=3x+8y\) ta được
\(x^3=11x\)\(\Leftrightarrow x\left(x^2-11\right)=0\)\(\Leftrightarrow\left[{}\begin{matrix}x=y=0\\x=y=\sqrt{11}\\x=y=-\sqrt{11}\end{matrix}\right.\)
NQ
1
AH
Akai Haruma
Giáo viên
31 tháng 3 2023
Lời giải:
Trừ theo vế 2 pt trên ta có:
$x^3-y^3=5y-5x$
$\Leftrightarrow (x-y)(x^2+xy+y^2)+5(x-y)=0$
$\Leftrightarrow (x-y)(x^2+xy+y^2+5)=0$
Ta thấy: $x^2+xy+y^2+5=(x+\frac{y}{2})^2+\frac{3y^2}{4}+5\geq 5>0$ với mọi $x,y$
$\Rightarrow x-y=0$
$\Leftrightarrow x=y$.
Thay vào pt (1): $x^3=3x+8x=11x$
$\Leftrightarrow x(x^2-11)=0$
$\Leftrightarrow x\in\left\{0; \pm \sqrt{11}\right\}$
Vậy........
7 tháng 3 2022
\(\left\{{}\begin{matrix}5x=5m\\y=2x-m+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=m\\y=10-m+1=11-m\end{matrix}\right.\)
Thay vào ta đc
\(2m^2-3\left(11-m\right)=2\Leftrightarrow2m^2-33+3m=2\Leftrightarrow2m^2+3m-35=0\Leftrightarrow m=\dfrac{7}{2};m=-5\)
T
6 tháng 10 2019
Lấy pt trên - pt dưới:
\(x^3-y^3=-5\left(x-y\right)\)
\(\Leftrightarrow\left(x-y\right)\left(x^2+y^2+xy+5\right)=0\)
Ta có: \(x^2+y^2+xy+5=\left(x+\frac{y}{2}\right)^2+\frac{3y^2}{4}+5>0\)
Do đó x = y. Thay vào pt thứ nhất thu được:
\(x^3=11x\Leftrightarrow x\left(x-\sqrt{11}\right)\left(x+\sqrt{11}\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=\sqrt{11}\\x=-\sqrt{11}\end{matrix}\right.\) (chú ý có 3 nghiệm lận nhé, nhiều khi trang web hay lỗi này nó hiển thị thiếu@@)
Suy ra y...
P/s: Em làm đúng không:)
CM
17 tháng 8 2019
Ta có
8 x + 7 y = 16 8 x − 3 y = − 24 ⇔ 8 x + 7 y = 16 8 x + 7 y − 8 x − 3 y = 16 − − 24 ⇔ 8 x + 7 y = 16 10 y = 40 ⇔ y = 4 8 x + 7.4 = 16 ⇔ y = 4 x = − 3 2
Vậy hệ phương trình có nghiệm duy nhất ( x ; y ) = − 3 2 ; 4
Đáp án: A
oán lớp 9 lớp 7 sao giúp