Tính : 1/3+1/3^2+1/3^3+...+1/3^50+1/3^51
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LV
0
13 tháng 4 2022
E=-1/3+1/3^2-1/3^3+1/3^4-...+1/3^50-1/3^51
3E=-1+1^2-1^3+1^4-1^5+...+1^50-1^51
3E=-1+1-1+1-1+...+1-1
3E=0
NT
1
29 tháng 10 2023
B=-1/3+1/3^2-.....-1/3^51
3B=-1/3^2+1/3^3-.....-1/3^52
3B-B=(-1/3^2+1/3^3-....-1/3^52)-(-1/3+1/3^2-....-1/3^51)
2B= -1/3^52-1/3
2B= -1/3^52-3^51/3^52
2B= -1-3^51/3^52
B= -3^51-1/3^52x2
2 tháng 3 2017
Từ dãy trên ta có:
(\(\frac{3}{2}\)+\(\frac{1}{2}\))+(\(\frac{8}{3}\)+\(\frac{2}{3}\))+......+(\(\frac{2600}{51}\)+\(\frac{1}{51}\)) < vì không có cách nhập hỗn số nên mình đổi ra phân số >
= 2 + 3 + 4 + 5 + 6 + ..........................+ 51
Từ 2 -> 51 có :( 51 - 2 ) : 1 + 1 = 50 số
Chia ra : 50 : 2 = 25 cặp
ta có( 51 + 2 ) x 25 =1325
Vậy tổng trên có kết quả bằng 1325 (tớ chỉ nghĩ thế thôi chứ sai đừng trách nhá.Đùa thôi,đúng đấy )
26 tháng 5 2022
\(B=\dfrac{1}{3}+\dfrac{1}{3^2}-\dfrac{1}{3^3}+...+\dfrac{1}{3^{50}}-\dfrac{1}{3^{51}}\)
\(=\dfrac{1}{\left(-3\right)}+\dfrac{1}{\left(-3\right)^2}+\dfrac{1}{\left(-3\right)^3}+...+\dfrac{1}{\left(-3\right)^{50}}+\dfrac{1}{\left(-3\right)^{51}}-\dfrac{1}{3}\)
\(=\dfrac{1}{\left(3\right)^2}+\dfrac{1}{\left(3\right)^3}+...+\dfrac{1}{\left(-3\right)^{51}}+\dfrac{1}{\left(-3\right)^{52}}\)
\(\Rightarrow\dfrac{4}{3}B=\dfrac{1}{-3}-\dfrac{1}{\left(-3\right)^{52}}=\dfrac{-3^{51}-1}{3^{52}}\Rightarrow B=\dfrac{-3^{51}-1}{4.3^{51}}\)
TT
0
M
1
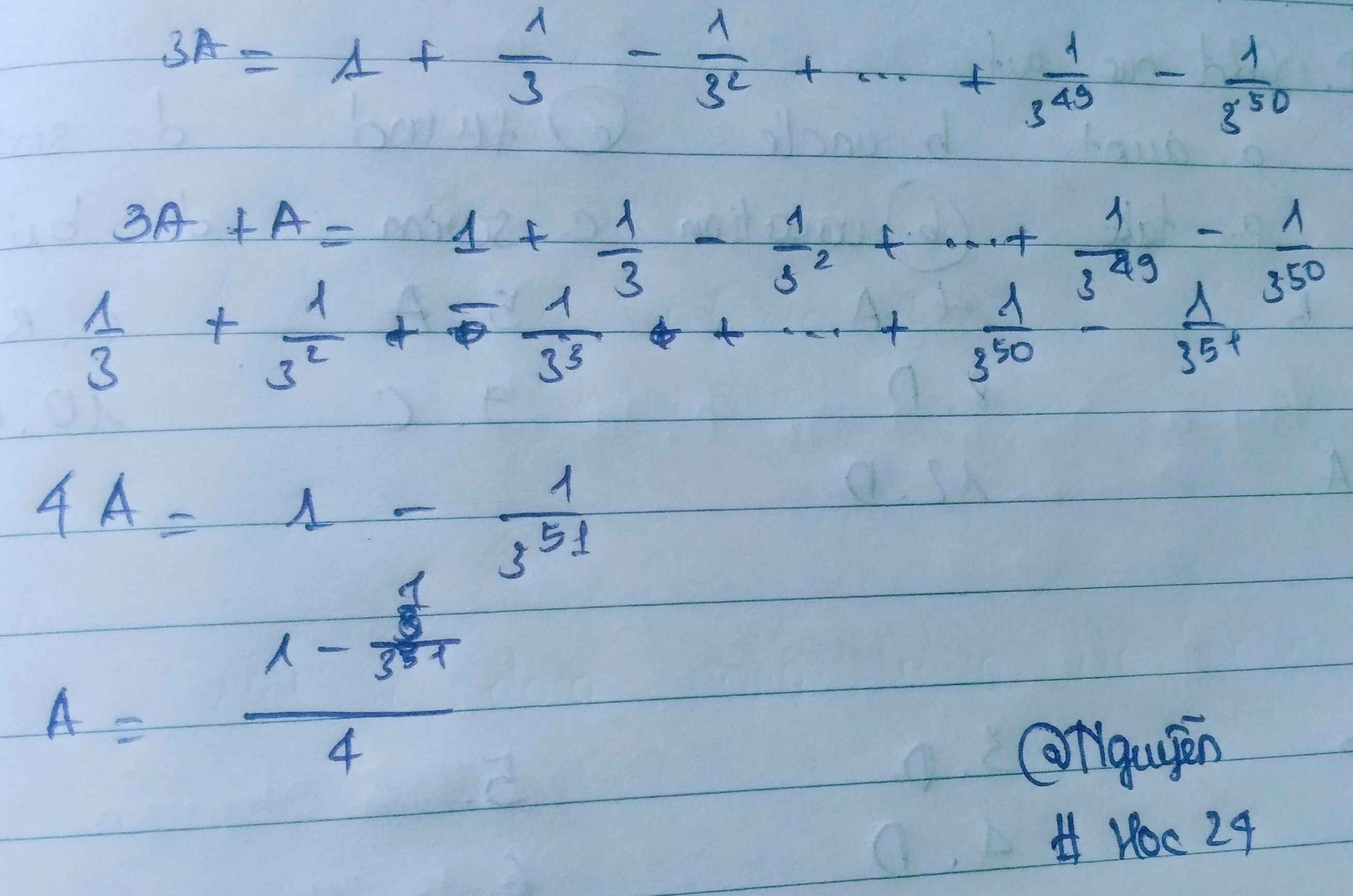
-----A=-1/3+1/3^2-1/3^3+-----+1/3^50-1/...
A*1/3 =-1/3^2+1/3^3+--------------------+1/3^5...
--------A=-1/3+1/3^2-1/3^3+...+1/3^50-1...
-------A*1/3 =-1/3^2+1/3^3+..---------...+1/3^51-1/3^...
---------------------------------------...
A+A*1/3=-1/3+0...+0+...0---------------...
A+A*1/3= -1/3-1/3^52
4/3*A= -1/3-1/3^52
Vậy
A= -(1/3+1/3^52)*3/4.