Giải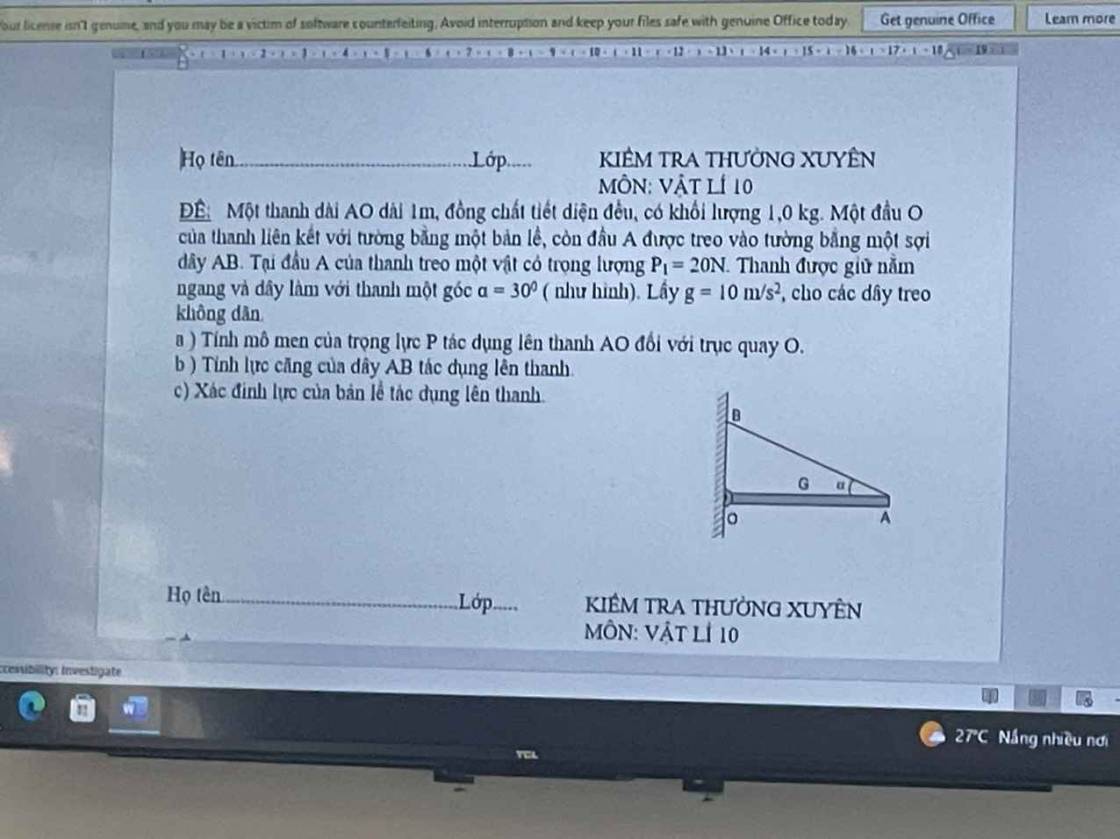
Giải chi tiết giúp mình câu c với ạ.Mình cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
giúp mình với ạ.Mình cần lời giải chi tiết
LA
25 tháng 4 2022
a) xét delta phẩy ta có b'2 - ac
<=> 4 - m
b) để pt 1 luôn có nghiệm thì delta phẩy ≥ 0
=> 4-m ≥ 0 => m ≤ 4
c) xét delta phẩy của pt (1) ta có
4 - m để pt có 2 nghiệm x1,x2 thì delta phẩy ≥ 0 => m ≤ 4
theo Vi-ét ta có:\(\left\{{}\begin{matrix}x1+x2=4\\x1x2=m\end{matrix}\right.\)
theo bài ra ta có: x12 + x22 = 12 <=> ( x1+x2 )2 - 2x1x2 = 12
<=> 16 - 2m -12 = 0 <=> 2m = 4 <=> m = 2 ( thỏa đk)
vậy m = 2 thì pt thỏa mãn điều kiện.
d) A= x12 + x22
<=> A = (x1+x2)2 - 2x1x2
<=> A = 16 - 2m ta có m ≤ 4
nên giá trị lớn nhất của m = 4
vậy giá trị nhỏ nhất của A = 16 - 2.4
GTNN của A = 8 dấu "=" xảy ra khi m = 4
25 tháng 4 2022
a) Ta có: a = 1 ; b' = -2 ; c = m
⇒ △' = b'2 - ac = ( -2 )2 - 1 .m = 4 - m
b) Để phương trình luôn có nghiệm thì △' \(\ge\) 0
⇒ 4 - m \(\ge\) 0 ⇔ m \(\le\) 4
Vậy khi m \(\le\) 4 thì phương trình luôn có nghiệm
c) Theo câu (b) thì phương trình luôn có nghiệm khi m \(\le\) 4
Theo hệ thức Vi - ét ta có: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=4\\x_1x_2=\dfrac{c}{a}=m\end{matrix}\right.\)
Do đó:
\(x_1^2+x_2^2=12\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=12\)
\(\Leftrightarrow4^2-2m=12\)
\(\Leftrightarrow4=2m\Leftrightarrow m=2\)
Vậy khi m = 2 thì phương trình (1) có 2 nghiệm x1 ; x2 thỏa mãn x12 + x22 = 12
VV
3
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 9 2021
b.
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}cos2x-\dfrac{1}{2}sin2x=-cosx\)
\(\Leftrightarrow cos\left(2x+\dfrac{\pi}{6}\right)=cos\left(x+\pi\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+\dfrac{\pi}{6}=x+\pi+k2\pi\\2x+\dfrac{\pi}{6}=-x-\pi+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{6}+k2\pi\\x=-\dfrac{7\pi}{18}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
c.
\(\Leftrightarrow2cos4x.sin3x=2sin4x.cos4x\)
\(\Leftrightarrow cos4x\left(sin4x-sin3x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos4x=0\\sin4x=sin3x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=\dfrac{\pi}{2}+k\pi\\4x=3x+k2\pi\\4x=\pi-3x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\\x=k2\pi\\x=\dfrac{\pi}{7}+\dfrac{k2\pi}{7}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 9 2021
2.
\(f\left(x\right)=\dfrac{1}{2}-\dfrac{1}{2}cos2x-\dfrac{\sqrt{3}}{2}sin2x-5\)
\(=-\dfrac{9}{2}-\left(\dfrac{1}{2}cos2x+\dfrac{\sqrt{3}}{2}sin2x\right)\)
\(=-\dfrac{9}{2}-cos\left(2x-\dfrac{\pi}{3}\right)\)
Do \(-1\le-cos\left(2x-\dfrac{\pi}{3}\right)\le1\Rightarrow-\dfrac{11}{2}\le y\le-\dfrac{7}{2}\)
\(y_{min}=-\dfrac{11}{2}\) khi \(cos\left(2x-\dfrac{\pi}{3}\right)=1\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\)
\(y_{max}=-\dfrac{7}{2}\) khi \(cos\left(2x-\dfrac{\pi}{3}\right)=-1\Rightarrow x=\dfrac{2\pi}{3}+k\pi\)
WY
0
HV
3
10 tháng 9 2023
3d:
20<x<45
x chia 4 dư 1 nên x-1 thuộc B(4)
=>\(x-1\in\left\{0;4;...;44;48\right\}\)
=>\(x\in\left\{1;5;...;45;49\right\}\)
mà 20<x<45
nên x thuộc {21;26;31;35;41}
4:
a: A={x∈N|51<=x<=127}
b: B={x∈N|100<=x<=999}
c: C={x∈N|x=7k+5; 0<=k<=8}
TK
3 tháng 12 2021
Câu 4:
a, Lực hấp dẫn giữa 2 quả cầu
\(F_{hd}=G\cdot\dfrac{m_1m_2}{d^2}=6,67\cdot10^{-11}\cdot\dfrac{20\cdot45}{3^2}=6,67\cdot10^{-9}\left(N\right)\)
b,Để trọng lượng giảm đi một nửa
Thì \(\dfrac{F_{hd}}{F_{hd}'}=\dfrac{G\cdot\dfrac{m^1m^2}{h^2}}{G\cdot\dfrac{m_1m_2}{h'^2}}=\dfrac{h'^2}{h^2}=\dfrac{F_{hd}}{\dfrac{F_{hd}}{2}}=2\Rightarrow2h^2=h'^2\Rightarrow\sqrt{2}h=h'^2\)
Vậy ...
MK
1
26 tháng 10 2023
a: \(A=\dfrac{x^2-\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}+\dfrac{2\left(x-1\right)}{\sqrt{x}-1}\)
\(=\dfrac{\sqrt{x}\left(x\sqrt{x}-1\right)}{x+\sqrt{x}+1}-\dfrac{\sqrt{x}\left(2\sqrt{x}+1\right)}{\sqrt{x}}+\dfrac{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}-1}\)
\(=\dfrac{\sqrt{x}\left(x+\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{x+\sqrt{x}+1}-2\sqrt{x}-1+2\sqrt{x}+2\)
\(=\sqrt{x}\left(\sqrt{x}-1\right)+1=x-\sqrt{x}+1\)
b:
\(\dfrac{x}{12}=\dfrac{\left(\sqrt{5}+2\right)\sqrt[3]{17\sqrt{5}-38}}{\sqrt{5}+\sqrt{14-6\sqrt{5}}}\)
\(\Leftrightarrow x\cdot\dfrac{1}{12}=\dfrac{\left(\sqrt{5}+2\right)\left(\sqrt{5}-2\right)}{\sqrt{5}+3-\sqrt{5}}\)
\(\Leftrightarrow\dfrac{x}{12}=\dfrac{1}{3}\)
=>x=36
Khi x=36 thì \(A=36-6+1=37-6=31\)
c: \(B=\dfrac{2\sqrt{x}}{A}=\dfrac{2\sqrt{x}}{x-\sqrt{x}+1}\)
\(B-2=\dfrac{2\sqrt{x}-2x+2\sqrt{x}-2}{x-\sqrt{x}+1}\)
\(=\dfrac{-2x+4\sqrt{x}-2}{x-\sqrt{x}+1}=\dfrac{-2\left(x-2\sqrt{x}+1\right)}{x-\sqrt{x}+1}\)
\(=\dfrac{-2\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{3}{4}}< 0\)
=>B<2
\(2\sqrt{x}>0;x-\sqrt{x}+1=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)
=>B>0
=>0<B<2
KT
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
1
14 tháng 10 2021
Bài 4:
b: Xét ΔABK vuông tại A có AD là đường cao ứng với cạnh huyền BK
nên \(BD\cdot BK=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)
2T
1
LP
Lê Phương Thảo
Giáo viên
17 tháng 3 2022
nKMnO4 = 14,2/158 ≃ 0,0899 mol
2KMnO4 + 16HCl → 2KCl + 2MnCl2 + 5Cl2 + 8H2O
0,0899 \(\dfrac{0,0899\times5}{2}\)
→ nCl2 = 0,22475 mol → VCl2 = 22,4.nCl2 = 5,0344 lít
BB
1
6 tháng 1 2023
Bài 5:
a: 2x-(3-5x)=4(x+3)
=>2x-3+5x=4x+12
=>7x-3=4x+12
=>3x=15
=>x=5
b: =>5/3x-2/3+x=1+5/2-3/2x
=>25/6x=25/6
=>x=1
c: 3x-2=2x-3
=>3x-2x=-3+2
=>x=-1
d: =>2u+27=4u+27
=>u=0
e: =>5-x+6=12-8x
=>-x+11=12-8x
=>7x=1
=>x=1/7
f: =>-90+12x=-45+6x
=>12x-90=6x-45
=>6x-45=0
=>x=9/2