Question

[Trần Bảo Nhi]

Cho hình thoi ABCD tâm O có AC = 8, BD = 6. Chọn hệ trục toạ độ (O;\(\overrightarrow{i}\);\(\overrightarrow{j}\)) sao cho \(\overrightarrow{i}\) và \(\overrightarrow{j}\) lần lượt cùng hướng với \(\overrightarrow{OB}\), \(\overrightarrow{OC}\)

a. Tìm toạ độ của các đỉnh của hình thoi ABCD.

b. Gọi I là trung điểm của BC và I' đói xứng với I qua O. Chứng minh A, I', D thẳng hàng.

Answer 1

[Lê Song Phương]

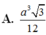
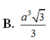
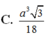
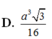
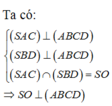
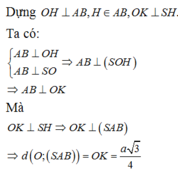
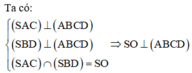
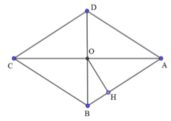
a) Từ đồ thị, ta thấy \(A\left(0;4\right),B\left(3;0\right),C\left(0;-4\right),D\left(-3;0\right)\)

b) Ta thấy O đồng thời là trung điểm của AC và II' nên AICI' là hình bình hành \(\Rightarrow\) AI' // CI hay AI' // BC (do B, I, C thẳng hàng)

 Tương tự, ta chứng minh được DI' // BC. Do đó A, I', D thẳng hàng theo tiên đề Euclide.