Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
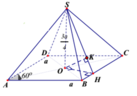
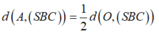
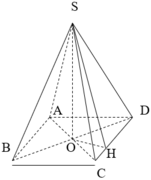
AC cắt (SBC) tại C , O là trung điểm AC =>khoảng cách
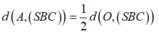
* Trong (ABCD) dựng OH ⊥ BC, trong (SOH) dựng OK ⊥ SH ta chứng minh được OK ⊥ (SBC)
=> khoảng cách d(O,(SBC))= OK.
∆ O B C vuông tại O có OH đường cao
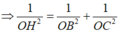
∆ S O H vuông tại O có OK đường cao
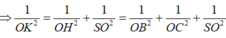
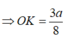
Vậy
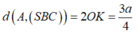

a: AC vuông góc BD
AC vuông góc SO
=>AC vuông góc (SBD)
b: (SA;(SBD))=(SA;SO)=gócASO
Xét ΔACB có BA=BC và góc ABC=60 độ
nên ΔBAC đều
=>AO=a/2
\(SA=\sqrt{SO^2+OA^2}=\sqrt{a^2+\dfrac{1}{4}a^2}=\dfrac{\sqrt{5}}{2}\cdot a\)
sin ASO=OA/SA=a/2:a*căn 5/2
\(=\dfrac{\sqrt{5}}{5}\)
=>góc ASO=27 độ

Đáp án A
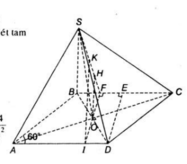
Trong mặt phẳng dựng đường thẳng đi qua A và vuông góc vưới SB tại K
Ta chứng minh được
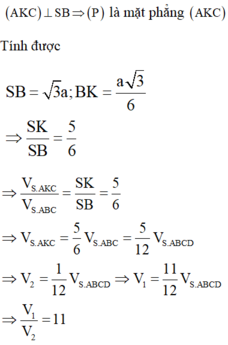

a: Xét ΔBAC có BA=BC và góc ABC=60 độ
nên ΔABC đều
=>\(S_{ABC}=\dfrac{a^2\sqrt{3}}{4}\)
=>\(S_{ABCD}=\dfrac{a^2\sqrt{3}}{2}\)
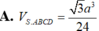
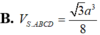
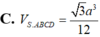
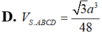
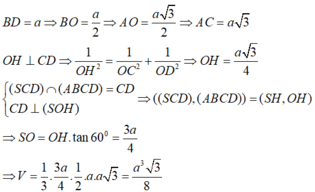

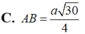

Lời giải:
$\widehat{BAD}=60^0\Rightarrow \widehat{BAO}=30^0$
$\frac{BO}{AB}=\sin \widehat{BAO}=\sin 30^0=\frac{1}{2}$
$\Rightarrow BO=\frac{AB}{2}=\frac{a}{2}$
$BD=2BO=a$
$\frac{AO}{AB}=\cos \widehat{BAO}=\cos 30^0=\frac{\sqrt{3}}{2}$
$\Rightarrow AO=\frac{\sqrt{3}a}{2}$
$\Rightarrow AC=\sqrt{3}a$
$S_{ABCD}=\frac{BD.AC}{2}=\frac{\sqrt{3}a^2}{2}$
$V_{S.ABCD}=\frac{1}{3}.SO.S_{ABCD}=\frac{1}{3}.\frac{3a}{4}.\frac{\sqrt{3}a^2}{2}=\frac{\sqrt{3}a^3}{8}$