Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
Cách 1:
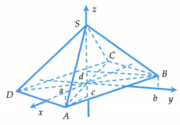
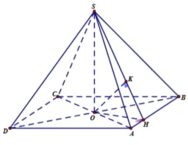
Lấy mặt phẳng α vuông góc với SO cắt (SAC), (SBD) theo các giao tuyến x’Ox, y’Oy.
![]()
Chọn hệ tọa độ Oxyz sao cho tia Oz trùng với tia OS
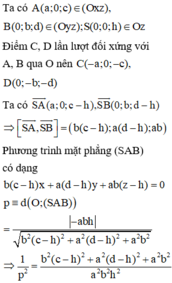
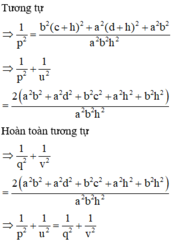

Cách 2:
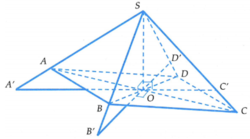
Trong mặt phẳng (SAC) dựng đường thẳng qua O vuông góc với đường thẳng SO cắt hai đường thẳng SA, SC lần lượt tại A’, C’
Trong mặt phẳng (SBD) dựng đường thẳng qua O vuông góc với đường thẳng SO cắt hai đường thẳng SB, SD lần lượt tại B’, D’
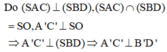
Khi đó tứ diện OSA’B’ có OS, OA’, OB’ đôi một vuông góc nên ta chứng minh được
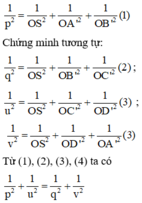
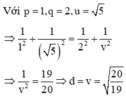

Đáp án B

Vì (SAB),(SAC) cùng vuông góc với (ABCD) nên giao tuyến S A ⊥ A B C D
Do AB, SB cùng vuông góc với giao tuyến BC của (ABCD) và (SBC) nên góc giữa hai mặt phẳng trên là góc:
S B A = 60 0 ⇒ S A = A B . sin 60 0 ⇒ S A = a 3 2
Vậy:
V S . A B C = 1 3 S A . A B . B C = 1 3 a 3 2 . a .3 a 2 = a 3 3 4

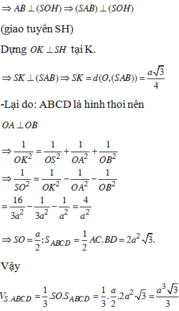
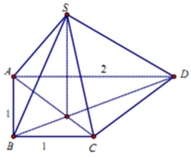
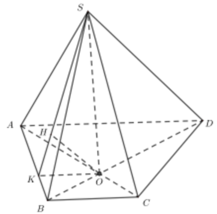

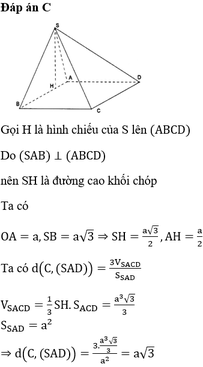

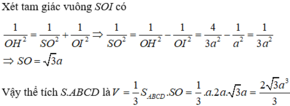
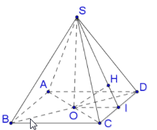

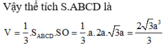

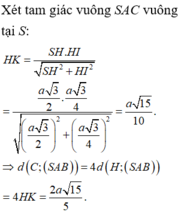
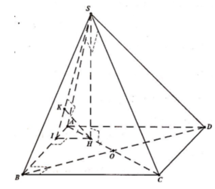
Chọn B.