Rút gọn biểu thức: \(A = \frac{{ \sin 2x }}{{1+ \cos 2x }} \)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
A
1
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
28 tháng 8 2018
\(=\frac{\sin^2x}{1+\frac{\cos x}{\sin x}}+\frac{\cos^2x}{1+\frac{\sin x}{\cos x}}-1=\frac{\sin^3x}{\sin x+\cos x}+\frac{\cos^3x}{\sin x+\cos x}-1.\)
\(=\frac{\sin^3x+\cos^3x}{\sin x+\cos x}-1=\frac{\left(\sin x+\cos x\right).\left(\sin^2x-\sin x.\cos x+\cos^2x\right)}{\sin x+\cos x}-1\)
\(=1-\sin x.\cos x-1=-\sin x.\cos x\)
14 tháng 10 2021
\(B=\dfrac{1-4\sin^2x\cdot\cos^2x}{\sin^2x+2\sin x\cdot\cos x+\cos^2}+2\sin x\cdot\cos x\\ B=\dfrac{1-4\sin^2x\cdot\cos^2x}{2\sin x\cdot\cos x}+2\sin x\cdot\cos x\\ B=\dfrac{1-4\sin^2x\cdot\cos^2x+4\sin^2x\cdot\cos^2x}{2\sin x\cdot\cos x}=\dfrac{1}{2\sin x\cdot\cos x}\)
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 4 2021
Bạn kiểm tra lại đề bài câu 1, câu này chỉ có thể rút gọn đến \(2cot^2x+2cotx+1\) nên biểu thức ko hợp lý
Đồng thời kiểm tra luôn đề câu 2, trong cả 2 căn thức đều xuất hiện \(6sin^2x\) rất không hợp lý, chắc chắn phải có 1 cái là \(6cos^2x\)
NH
1
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 7 2020
\(=\frac{1+cosx}{sinx}\left(1-\frac{1+cos^2x-2cosx}{sin^2x}\right)=\frac{1+cosx}{sinx}\left(\frac{sin^2x-1-cos^2x+2cosx}{sin^2x}\right)\)
\(=\frac{1+cosx}{sinx}\left(\frac{-cos^2x-cos^2x+2cosx}{sin^2x}\right)=\frac{\left(1+cosx\right)2cosx\left(1-cosx\right)}{sinx.sin^2x}\)
\(=\frac{2cosx\left(1-cos^2x\right)}{sinx.sin^2x}=\frac{2cosx.sin^2x}{sinx.sin^2x}=\frac{2cosx}{sinx}=2cotx\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 5 2020
\(\frac{cos^2x\left(1+cot^2x\right)}{sin^2x\left(1+tan^2x\right)}=\frac{tan^2x\left(1+cot^2x\right)}{1+tan^2x}=\frac{tan^2x+tan^2x.cot^2x}{1+tan^2x}=\frac{1+tan^2x}{1+tan^2x}=1\)
Câu b ko rút gọn được, bạn coi lại đề
\(x^2sin^2a+y^2cos^2a-2xy.sina.cosa+x^2cos^2a+y^2sin^2a+2xy.sinx.cosa\)
\(=x^2\left(sin^2a+cos^2a\right)+y^2\left(cos^2a+sin^2a\right)=x^2+y^2\)
TG
1
NA
Ngoc Anh Thai
Giáo viên
10 tháng 4 2021
\(A=\dfrac{sin^2x-cos^2x.\left(1-cos^2x\right)}{cos^2x-sin^2x.\left(1-sin^2x\right)}=\dfrac{sin^2x-cos^2x.sin^2x}{cos^2x-sin^2x.cos^2x}\\ =\dfrac{sin^2x.\left(1-cos^2x\right)}{cos^2x.\left(1-sin^2x\right)}=\dfrac{sin^2x.sin^2x}{cos^2x.cos^2x}=\dfrac{sin^4x}{cos^4x}.\)
NN
0
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2020
\(cos\left(2x+\frac{\pi}{6}\right)cos\left(2x-\frac{\pi}{6}\right)=\frac{1}{2}\left(cos4x+cos\frac{\pi}{3}\right)=\frac{1}{2}\left(cos4x+\frac{1}{2}\right)\)
\(sin\left(x+\frac{\pi}{6}\right)sin\left(x-\frac{\pi}{6}\right)=\frac{1}{2}\left(cos\frac{\pi}{3}-cos2x\right)=\frac{1}{2}\left(\frac{1}{2}-cos2x\right)\)
\(\Rightarrow C=\frac{1}{2}sinx.cos4x+\frac{1}{4}sinx+\frac{1}{4}sin3x-\frac{1}{2}sin3x.cos2x\)
\(=\frac{1}{4}sin5x-\frac{1}{4}sin3x+\frac{1}{4}sinx+\frac{1}{4}sin3x-\frac{1}{4}sin5x+\frac{1}{4}sinx\)
\(=\frac{1}{2}sinx\)
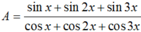
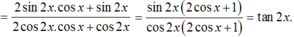
\(A = \frac{{ \sin 2x }}{{1+ \cos 2x }} = \frac{{2.\sin x.\cos x }}{{1+(2\cos ^2x-1)}} = \frac{{2.\sin x.\cos x }}{{2\cos ^2x}} = \frac{{\sin x}}{{\cos x}}= tanx\)