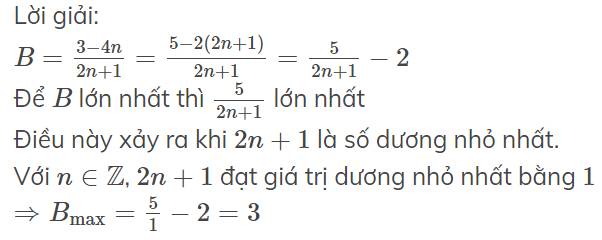Cho phân số B= 3-4n/2n+1 (n thuộc Z)
Tìm giá trị lớn nhất của B
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
QM
1
AH
Akai Haruma
Giáo viên
4 tháng 5 2023
Đúng(0)
Những câu hỏi liên quan
QM
1
QM
1
AH
Akai Haruma
Giáo viên
3 tháng 5 2023
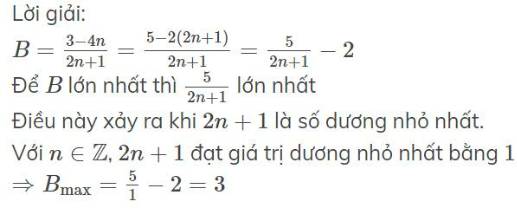
Lời giải:
$B=\frac{3-4n}{2n+1}=\frac{5-2(2n+1)}{2n+1}=\frac{5}{2n+1}-2$
Để $B$ lớn nhất thì $\frac{5}{2n+1}$ lớn nhất
Điều này xảy ra khi $2n+1$ là số dương nhỏ nhất.
Với $n\in\mathbb{Z}$, $2n+1$ đạt giá trị dương nhỏ nhất bằng $1$
$\Rightarrow B_{\max}=\frac{5}{1}-2=3$
W
29 tháng 7 2020
a, \(\frac{4n+1}{2n-3}=\frac{2n-3+2n+4}{2x-3}\)
= \(\frac{2n-3}{2n-3}+\frac{2n+4}{2n-3}\) = \(1+\frac{2n-3+7}{2n-3}=1+\frac{7}{2n-3}\)
để B tối giản thì 7 phải chia hết cho 2n - 3
=> 2n - 3 thuộc Ư(7)
=> 2n - 3 = { 1 , -1 , 7 , -7 }
=> 2n = { 4 , 2 , 10 , -4 }
=> n ={ 2 , 1 ,5 ,-2 }
Đừng bỏ cuộc
LV
0
LV
0
NT
2
HL
27 tháng 2 2015
Ta có:B=(4n+9)/(2n+3) =(2(2n+3)+3)/(2n+3)=2+(3/2n+3)
B lớn nhất khi và chỉ khi 3/2n+3 lớn nhất <=> 2n+3 nhỏ nhất (2n+3 >0)
n thuộc Z=> 2n+3 thuộc Z => 2n+3=1<=> n=-1
vậy,n=-1
9 tháng 5 2018
ahhhhhhhhhhhhhhhhhhhjkdhajksdhasjkdhkjashjkdkahduoyqdkjqwheyquwhsjkhksahdkhsakdssssssssssssssssssssssssssjhjhdjksahdjkhskajdhjbsajdhjkshadkhajkh bajshkb asdhjas n jsdhjkahkdhjsahkdhas jahdjka djakshdjksa d sajkdhajkshdjkhsdjkahdajkhdkj ad áhdjkash